In the given figure, PL⊥OA and PM⊥OB such that OL=OM. Prove that :
(i) ΔOLP≅ΔOMP
(ii) PL=PM
∠LOP=∠MOP

Step by step video & image solution for In the given figure, PLbotOA and PMbotOB such that OL=OM. Prove that : (i) DeltaOLP~=DeltaOMP (ii) PL=PM angleLOP=angleMOP by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the given figure, AB⊥BD,CD⊥BD and AB=CD. Prove that :
(i) ΔABD≅ΔCDB
(ii) AD-CB

View SolutionIn the given figure we have AO=BO and CO=DO. Prove that :
(i) ΔAOC≅ΔBOD
AC=BD

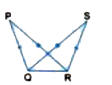
View SolutionIn the given figure, we have PQ=SR and PR=SQ. Prove that :
(i) ΔPQR≅ΔSRQ
(ii) ∠PQR=∠SRQ
View SolutionIn the given figure, AB=CD and AD=CB. Prove that :
(i) ΔABD=ΔCDB
(ii) ∠A=∠C

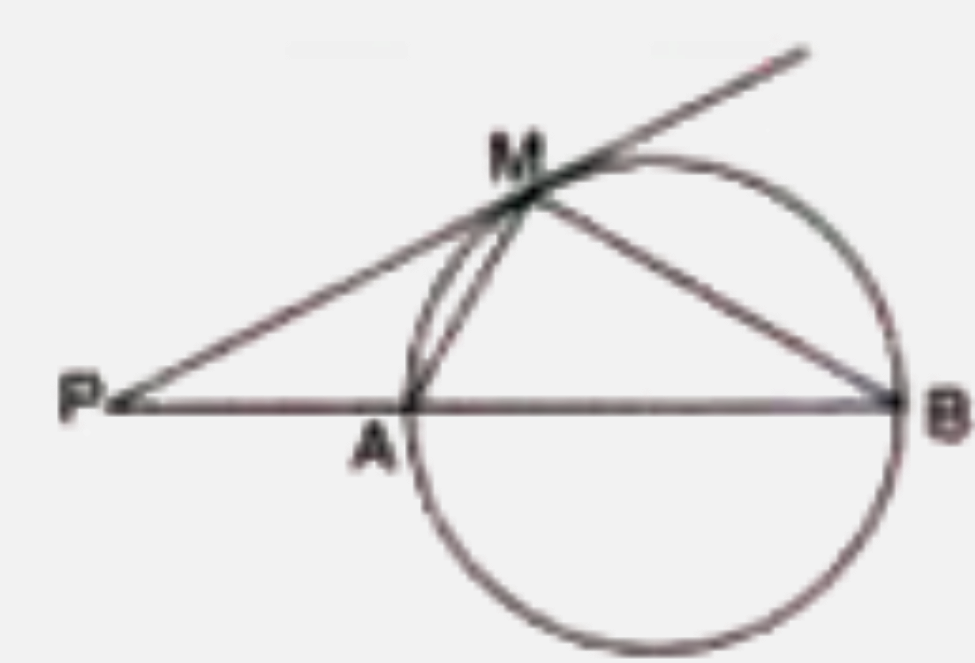
View SolutionIn the given figure PM is a tangent to the circle and PA =AM.
Prove that
(i) ΔPMB is isosceles
(ii) PAXxPB=MB2
View SolutionIn the given figure, AB and DE are perpendicular to BC.
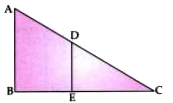
(i) Prove that ΔABC~ΔDEC
View SolutionIn the following figure, OA = OC and AB = BC. Prove that :
(i) ∠AOB=90∘
(ii) ΔAOD≅ΔCOD
(iii) AD = CD

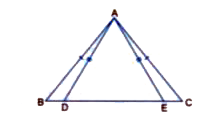
View SolutionIn the given figure AB=AC and AD=AE. Prove that (i) ΔABD≅ΔACE and (ii) BE=DC
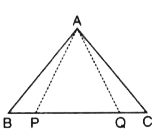
View SolutionThe given figure shows a ΔABC in which AB =AC and BP =CQ .
Prove that :
(i) ΔABQ≅ΔACP.
(ii) ΔAPQ is isosceles.
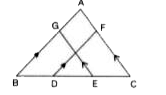
View SolutionIn the given figure : AB//FD, AC//GE and BD = CE, prove that :
(i) BG = DF
(ii) CF = EG
View Solution
