In the given figure PM is a tangent to the circle and PA =AM.
Prove that
(i) ΔPMB is isosceles
(ii) PAXxPB=MB2
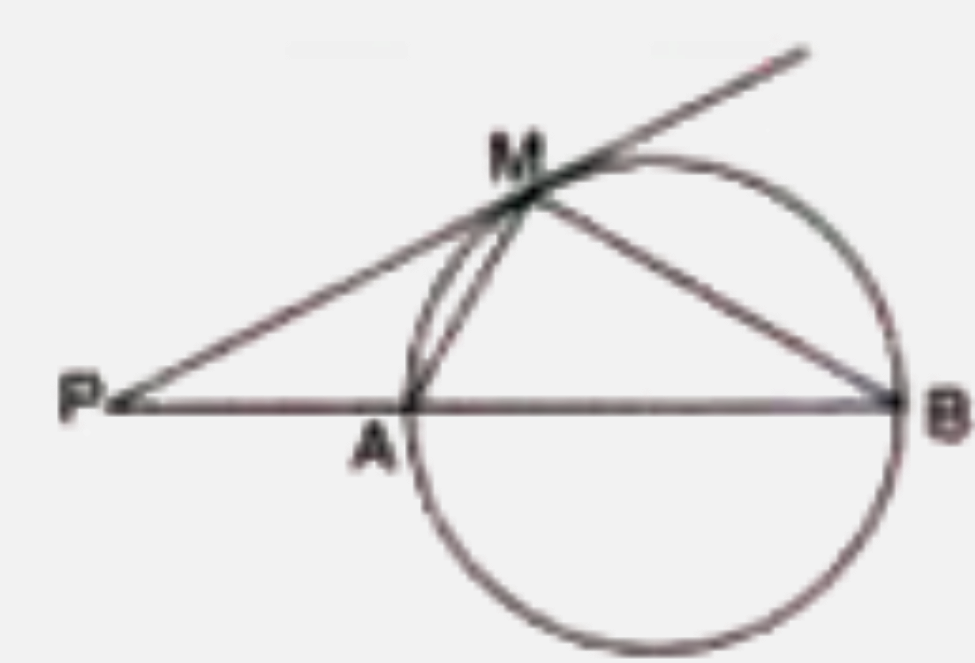
The correct Answer is:ΔPMBis isosceles
PA×BPb=MB2
Step by step video & image solution for In the given figure PM is a tangent to the circle and PA =AM. Prove that (i) DeltaPMB is isosceles (ii) PAXxPB=MB^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18(A)
24 Videos
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)
18 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
In the given figure
tangent PT=12.5 cm and PA=10cm, find AB.

View SolutionIn the given figure PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQand∠PAC. If ∠BAQ=30∘, prove that :
(i) BD is a diameter of the circle.
(ii) ABC is an isosceles triangle

View SolutionIn the figure PA is a tangent to the circle, PBC is secant and AD bisects angle BAC.
Show that triangle PAD is an isosceles triangle. Also, show that:
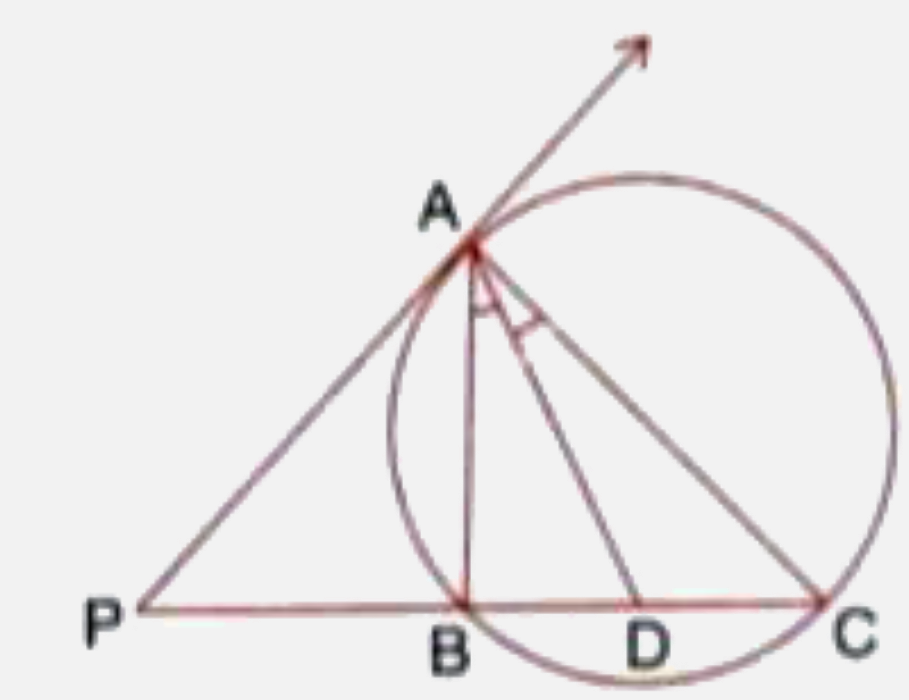
∠CAD=12[∠PBA−∠PAB]
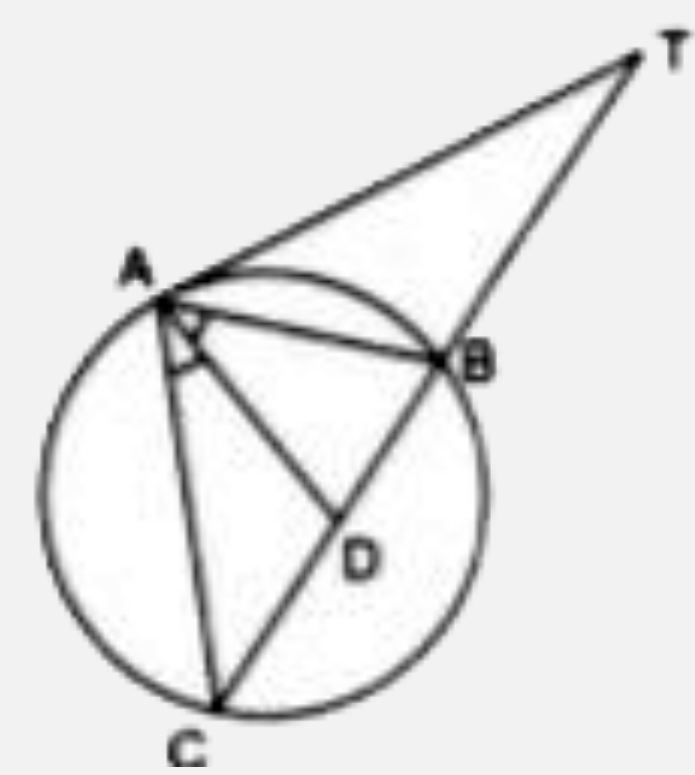
View SolutionIn the given TA is a tangent to the cirlce and TBC is a secant. If AD bisects angle BAC, prove that:ΔADT is isosceles.
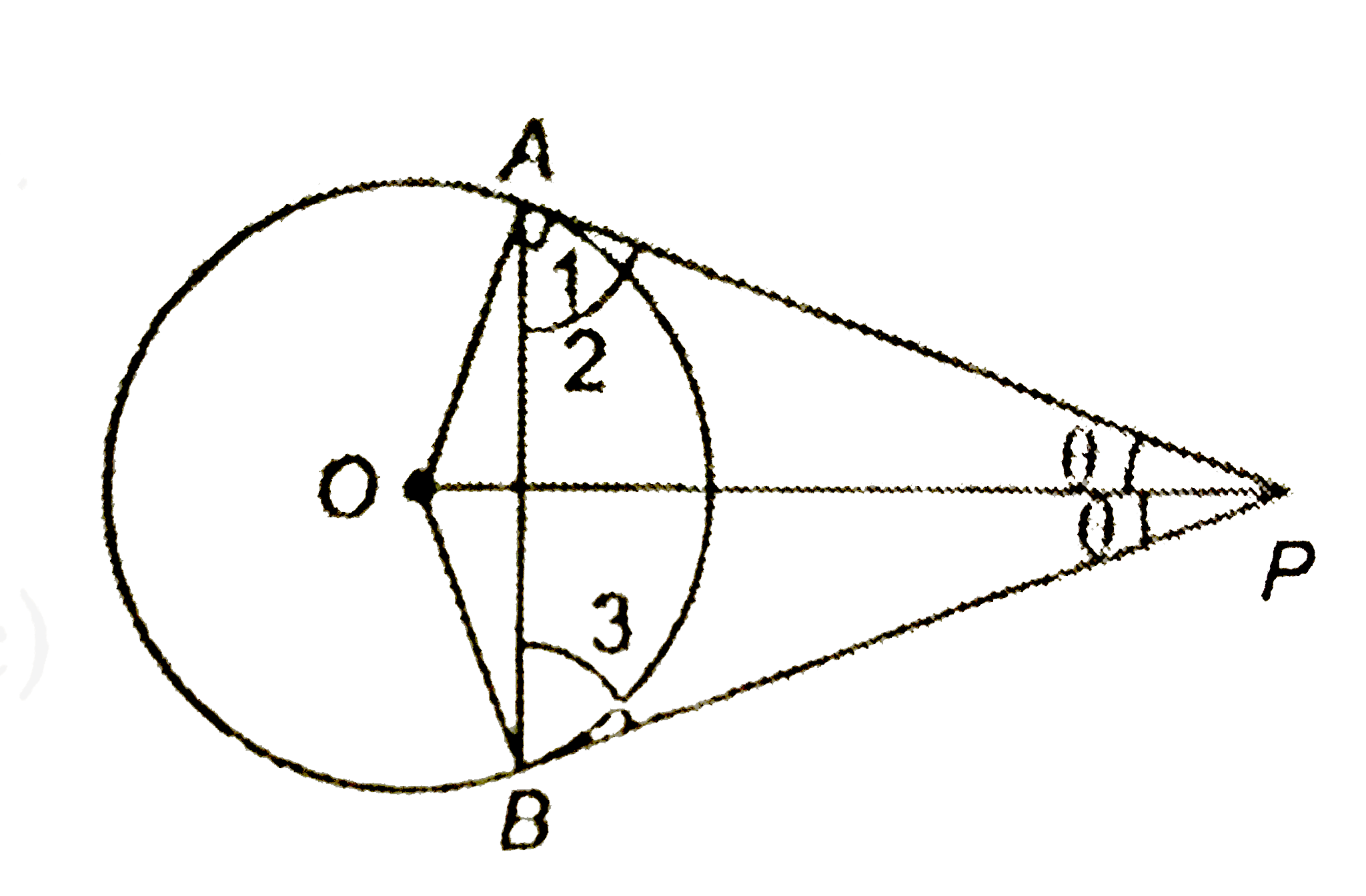
View SolutionIn the given figure, OP is equal to the diameter of the circle. Prove that △ABP is an equilateral triangle.
View SolutionIn the given figure, AB⊥BD,CD⊥BD and AB=CD. Prove that :
(i) ΔABD≅ΔCDB
(ii) AD-CB

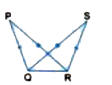
View SolutionIn the given figure, we have PQ=SR and PR=SQ. Prove that :
(i) ΔPQR≅ΔSRQ
(ii) ∠PQR=∠SRQ
View SolutionIn Figure, BC is a tangent to the circle with centre O.OE bisects AP. Prove that AEO~ABC.
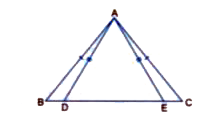
View SolutionIn the given figure AB=AC and AD=AE. Prove that (i) ΔABD≅ΔACE and (ii) BE=DC
View SolutionIn the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
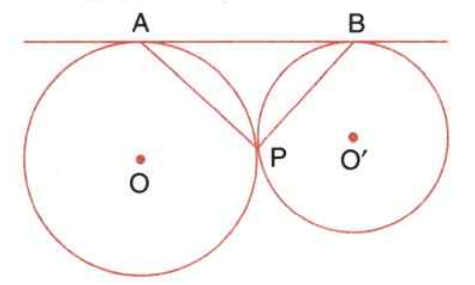
(i) tangent at point P bisects AB
(ii) angle APB=90∘
View Solution
