In the given figure, PQ, PR and ST are tangents to the same circle. If ∠P=40∘and∠QRT=75∘, find a, b and c
< 
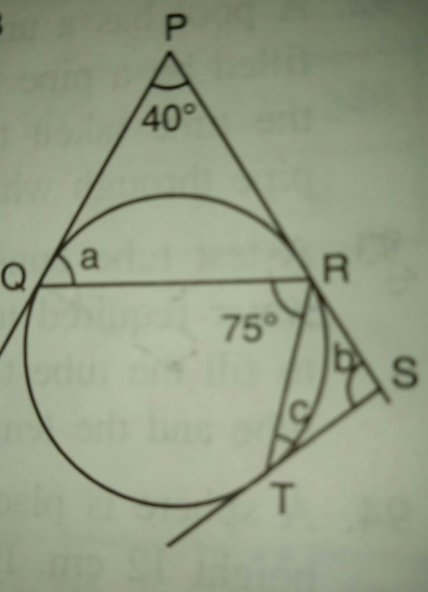
The correct Answer is:a=70∘,b=110∘andc=35∘
Step by step video & image solution for In the given figure, PQ, PR and ST are tangents to the same circle. If angleP= 40^(@) and angleQRT= 75^(@), find a, b and c < by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CONSTRUCTION)3videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (MENSURATION)8videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CIRCLES)9videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - BANKING (RECURRING DEPOSIT ACCOUNTS)EXERCISE - QUESTIONS7videos
BANKING (RECURRING DEPOSIT ACCOUNTS)
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )28videos
CIRCLES
Similar Questions
In the given figure , PR>PQ
Prove that : AR>AQ
View SolutionIn the given figure if PQ||YZ. Find XQ.
View SolutionIn the following figure PQ and PR are tangents to the circle with the centre O. If ∠QPR=60∘ calculate
(i)∠QOR
(ii) ∠OQR
(iii) ∠QSR
View SolutionIn the given graph, pq,pr and st represent
View SolutionIn the given diagram, PQ and RS are common tangents to the two circles with centres C and D. Find the length of PQ and hence area of trapexium RSDC.
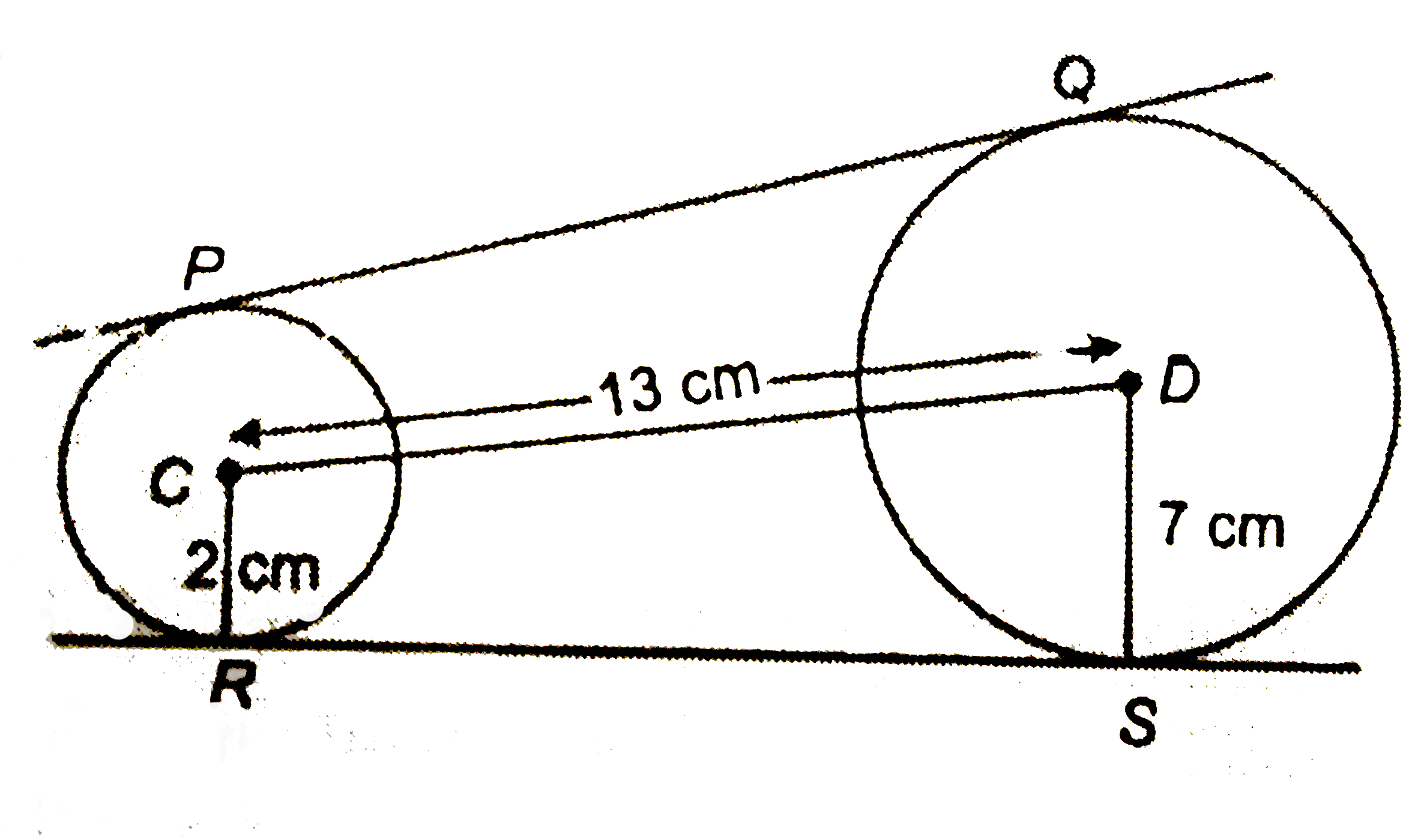
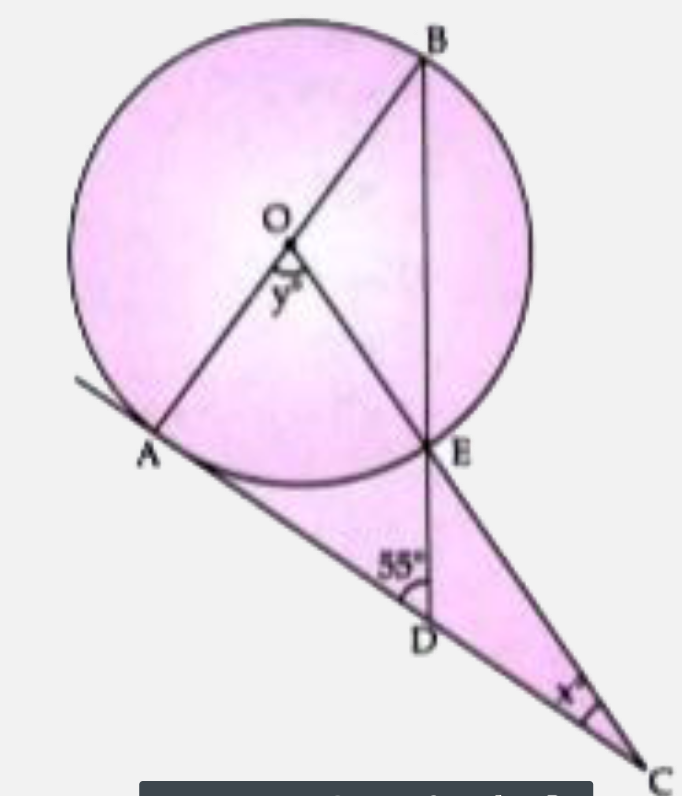
View SolutionIn the given figure AC is a tangent to the circle with centre O.
If ∠ADB=55∘, find x and y. Give reason for your answer.
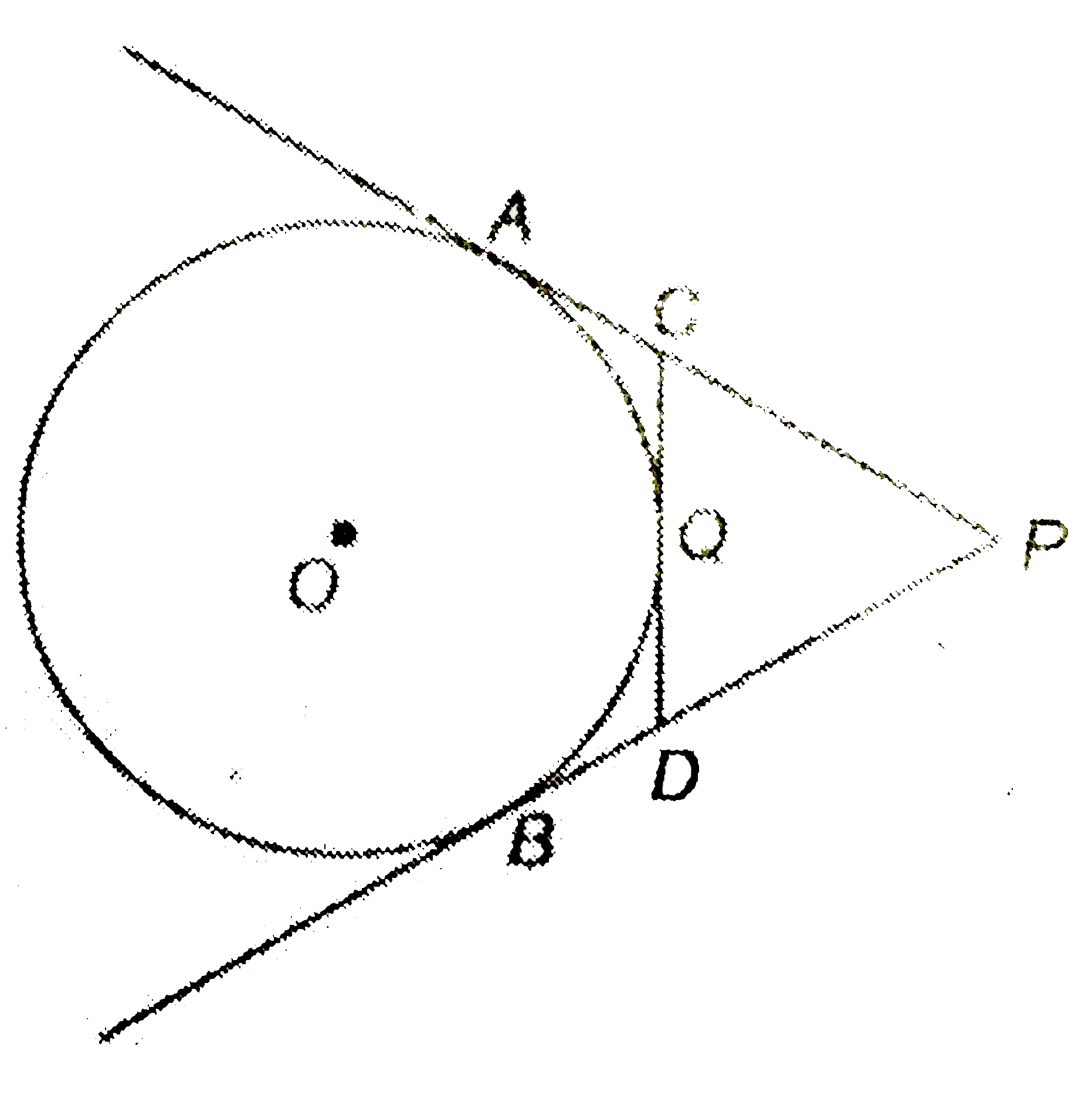
View SolutionIn the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA =12 cm, QC=3cm, then find PC+PD.
View SolutionIn the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
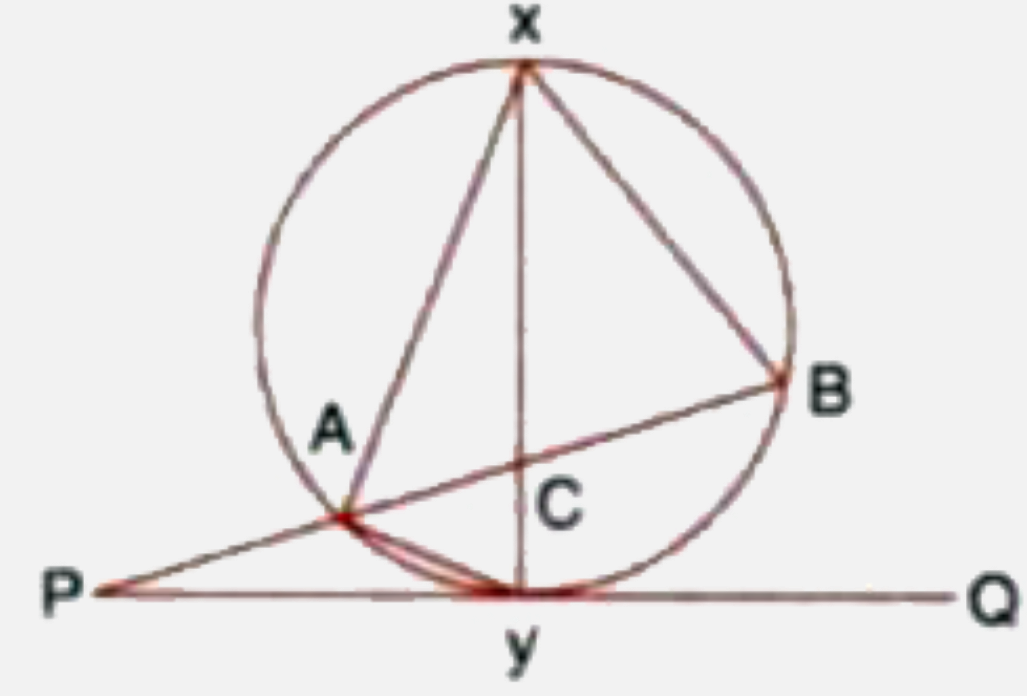
If ∠AXB=50∘ and ∠ABX=70∘ find ∠BAY and ∠APYView SolutionIn the given figure O is the centre of the circle. Tangents at A and B meets at C.
If ∠ACO=30∘, find
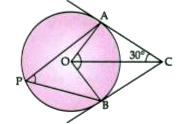
∠BCOView SolutionIn the given figure O is the centre of the circle. Tangents at A and B meets at C.
If ∠ACO=30∘, find
∠APBView Solution