In the given figure, two tangents PQ and PR are drawn to a circle with centre C from an external point P, Prove that ∠QPR=2∠OQR.
To prove that ∠QPR = 2 ∠OQR, we will follow a systematic approach using properties of tangents and triangles.
1. Identify the Tangents and Triangle:
- We have two tangents, PQ and PR, drawn from an external point P to a circle centered at C.
- Let the points where the tangents touch the circle be Q and R respectively.
2. Establish Tangent Lengths:
- By the property of tangents from an external point, we know that the lengths of the tangents drawn from a point outside the circle to the circle are equal. Therefore, we have:
PQ=PR
3. Recognize the Isosceles Triangle:
- Since PQ = PR, triangle PQR is an isosceles triangle. This implies that the angles opposite to the equal sides are also equal:
∠PQR=∠PRQ
4. Sum of Angles in Triangle PQR:
- The sum of angles in any triangle is 180 degrees. Thus, we can write:
∠PQR+∠PRQ+∠QPR=180∘
- Substituting the equal angles, we have:
∠PQR+∠PQR+∠QPR=180∘
- This simplifies to:
2∠PQR+∠QPR=180∘
5. Rearranging for QPR:
- Rearranging the equation gives:
∠QPR=180∘−2∠PQR
- This can also be rewritten as:
∠PQR=90∘−12∠QPR
6. Using the Perpendicularity:
- Since OQ is perpendicular to PQ (where O is the center of the circle), we have:
∠OQP=90∘
- This means:
∠OQR+∠PQR=90∘
- Rearranging gives:
∠OQR=90∘−∠PQR
7. Substituting for OQR:
- Now, substituting the expression for ∠PQR from step 5 into this equation:
∠OQR=90∘−(90∘−12∠QPR)
- This simplifies to:
∠OQR=12∠QPR
8. Final Result:
- From the equation above, we can multiply both sides by 2:
2∠OQR=∠QPR
- Therefore, we conclude:
∠QPR=2∠OQR
Conclusion:
Thus, we have proved that ∠QPR = 2 ∠OQR.
- We have two tangents, PQ and PR, drawn from an external point P to a circle centered at C.
- Let the points where the tangents touch the circle be Q and R respectively.
- By the property of tangents from an external point, we know that the lengths of the tangents drawn from a point outside the circle to the circle are equal. Therefore, we have:
PQ=PR
- Since PQ = PR, triangle PQR is an isosceles triangle. This implies that the angles opposite to the equal sides are also equal:
∠PQR=∠PRQ
- The sum of angles in any triangle is 180 degrees. Thus, we can write:
∠PQR+∠PRQ+∠QPR=180∘
- Substituting the equal angles, we have:
∠PQR+∠PQR+∠QPR=180∘
- This simplifies to:
2∠PQR+∠QPR=180∘
- Rearranging the equation gives:
∠QPR=180∘−2∠PQR
- This can also be rewritten as:
∠PQR=90∘−12∠QPR
- Since OQ is perpendicular to PQ (where O is the center of the circle), we have:
∠OQP=90∘
- This means:
∠OQR+∠PQR=90∘
- Rearranging gives:
∠OQR=90∘−∠PQR
- Now, substituting the expression for ∠PQR from step 5 into this equation:
∠OQR=90∘−(90∘−12∠QPR)
- This simplifies to:
∠OQR=12∠QPR
- From the equation above, we can multiply both sides by 2:
2∠OQR=∠QPR
- Therefore, we conclude:
∠QPR=2∠OQR
Thus, we have proved that ∠QPR = 2 ∠OQR.
Topper's Solved these Questions
Similar Questions
In the given figure, two tangents PQ and PR are drawn to a circle with centre O from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionIn Figure, two tangents ABandAC are drawn to a circle with centre O such that ∠BAC=1200. Prove that OA=2AB
View SolutionIn the given figure, from an external point P,two tangents PT and PS are drawn to a circle with centre O and radius r.If OP=2r, show that ∠OTS=∠OST=30∘
View SolutionFrom a point P , two tangents PA and PB are drawn to a circle with centre O . If OP= diameter of the circle, show that △APB is equilateral.
View SolutionTwo tangent segments PA and PB are drawn to a circle with centre O such that ∠APB=120∘ . Prove that OP=2 AP .
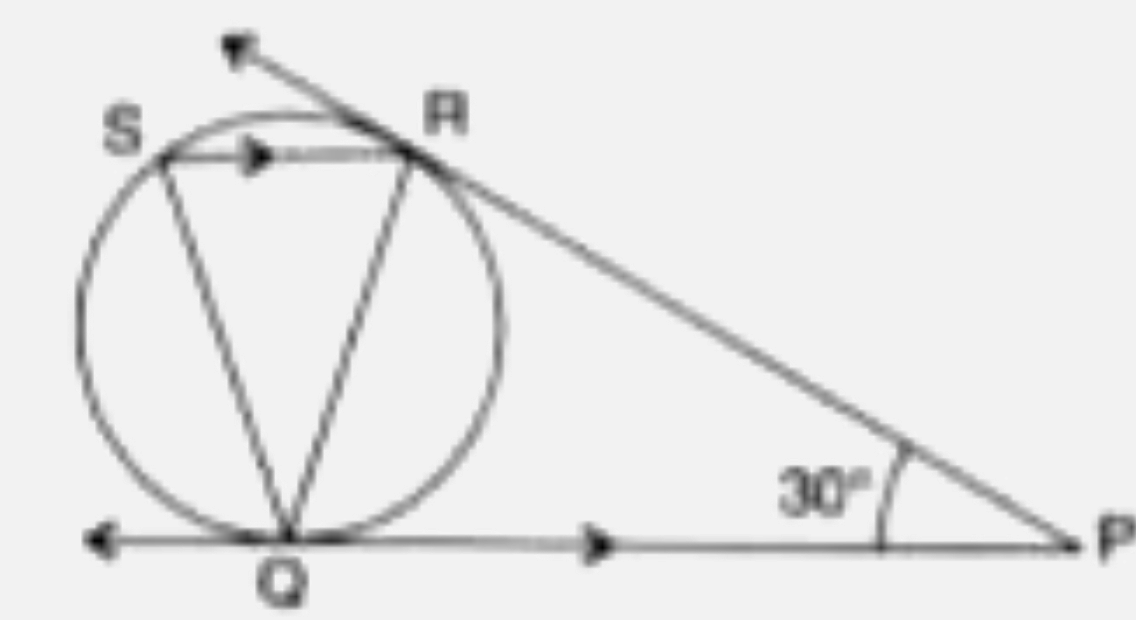
View SolutionIn the given figure, tangents PQ and PR are drawn to a circle such that angle RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the angle RQS.
 View Solution
View SolutionTwo circles touch externally at a point P. From a external point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. Prove that TQ=TR.
View SolutionFrom an external point P, two tangents, PA and PB are drawn to a circle with centre 0. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA=10 cm, find the perimeter of the triangle PCD.
View Solution

