Question

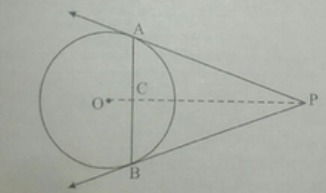
Two tangent
segments $PA$
and $PB$
are drawn
to a circle with centre $O$
such that $\angle APB={120}^{\circ }$
. Prove
that $OP=2AP$
.

Explanation

To solve the problem, we need to prove that $$OP=2\times AP$$ given that two tangents $$PA$$ and $$PB$$ are drawn to a circle with center $$O$$ such that $$\angle APB={120}^{\circ }$$.

1. Draw the Circle and Tangents:
- Draw a circle with center \( O \).
- Mark points \( A \) and \( B \) on the circle such that \( PA \) and \( PB \) are the tangent segments from point \( P \) to points \( A \) and \( B \) on the circle.

2. Label the Angles:
- Given that \( \angle APB = 120^\circ \).
- Since \( PA \) and \( PB \) are tangents to the circle, we know that \( OA \perp PA \) and \( OB \perp PB \). Therefore, \( \angle OAP = 90^\circ \) and \( \angle OBP = 90^\circ \).

3. Congruent Triangles:
- In triangles \( OAP \) and \( OBP \):
- \( OA = OB \) (both are radii of the circle),
- \( OP = OP \) (common side),
- \( \angle OAP = \angle OBP = 90^\circ \).
- By the SAS (Side-Angle-Side) criterion, \( \triangle OAP \cong \triangle OBP \).

4. Finding Angles:
- Since \( \triangle OAP \) is congruent to \( \triangle OBP \), we have:
\( \angle OPA = \angle OPB \)
- Let \( \angle OPA = \angle OPB = x \). Therefore:
\( x + x + 120^\circ = 180^\circ \quad (\text{sum of angles in triangle}) \)
- This simplifies to:
\( 2x + 120^\circ = 180^\circ \)
- Thus:
\( 2x = 60^\circ \implies x = 30^\circ \)

5. Using Cosine Rule:
- In triangle \( OAP \):
\( \cos(30^\circ) = \frac{AP}{OP} \)
- We know \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \), so:
\( \frac{\sqrt{3}}{2} = \frac{AP}{OP} \)
- Rearranging gives:
\( AP = \frac{\sqrt{3}}{2} OP \)

6. Finding the Relationship:
- From the cosine relation, we can express \( OP \) in terms of \( AP \):
\( OP = \frac{2}{\sqrt{3}} AP \)
- However, we need to express \( OP \) in terms of \( AP \) directly. Since we know that \( \angle OAP = 90^\circ \) and \( \angle OPA = 30^\circ \), we can also use the sine relation:
\( \sin(30^\circ) = \frac{AP}{OP} \)
- Since \( \sin(30^\circ) = \frac{1}{2} \):
\( \frac{1}{2} = \frac{AP}{OP} \implies OP = 2 \times AP \)

Conclusion:
Thus, we have proved that:
\( OP = 2 \times AP \)