Question

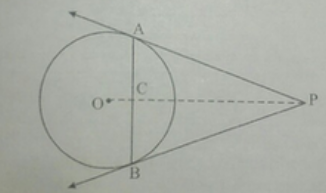
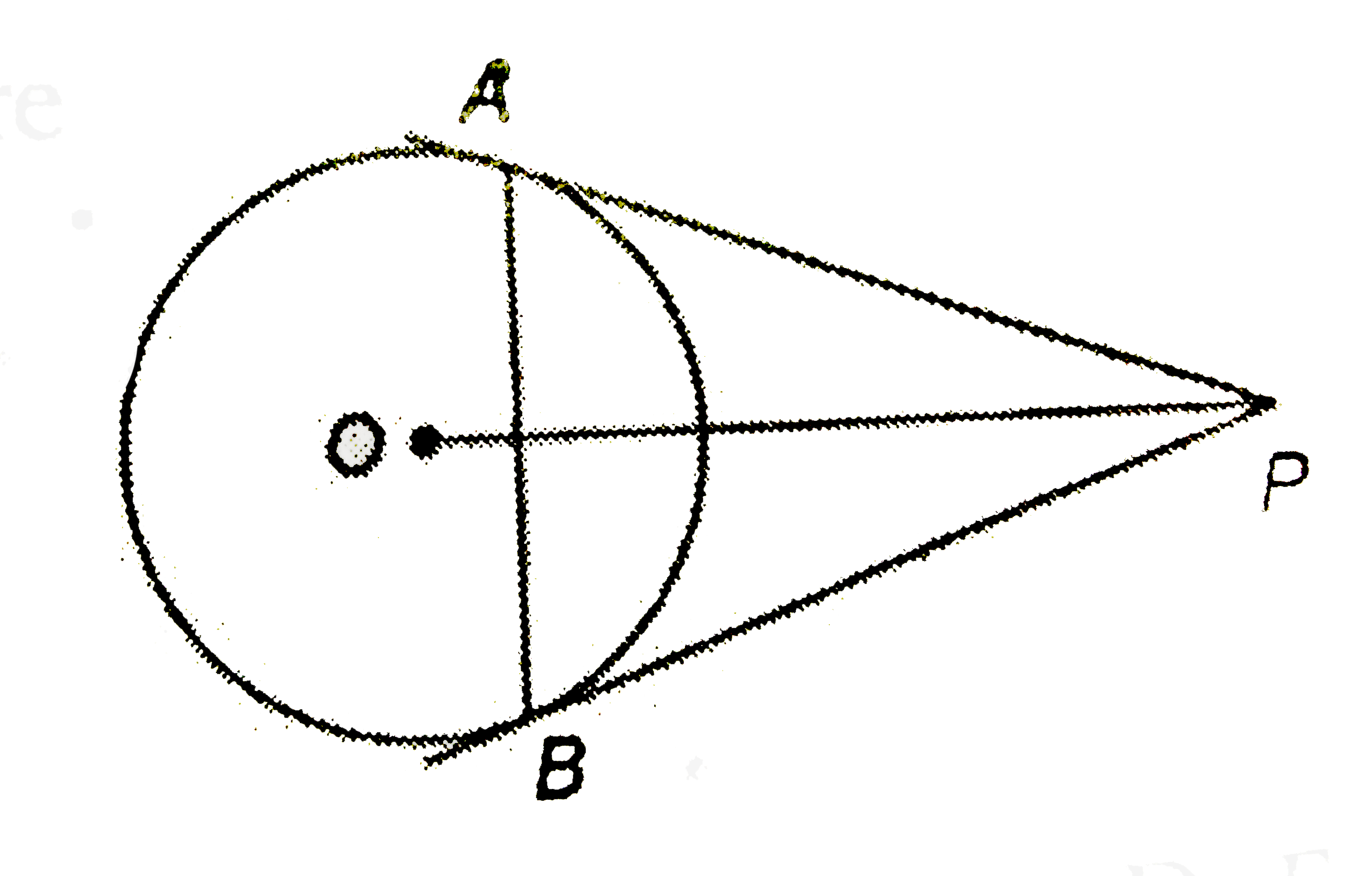
From an external point P, two tangents, PA and PB are drawn to a circle with centre 0. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA=10 cm, find the perimeter of the triangle PCD.

Explanation

To solve the problem step by step, we will follow the information provided in the question and use properties of tangents to circles.

Step 1: Understand the Problem
We have a circle with center O and an external point P from which two tangents PA and PB are drawn to the circle. We know that PA = 10 cm. A tangent at point E on the circle intersects PA at point C and PB at point D. We need to find the perimeter of triangle PCD.

Step 2: Draw the Diagram
Draw a circle with center O. Mark point P outside the circle. Draw the tangents PA and PB from point P to points A and B on the circle. Mark point E on the circle and draw the tangent line at E, which intersects PA at point C and PB at point D.

Step 3: Use the Tangent Properties
From the properties of tangents drawn from an external point:
- The lengths of the tangents from point P to points A and B are equal.
\( PA = PB = 10 \text{ cm} \)

Step 4: Apply the Tangent Segment Theorem
Since C and D are points where the tangent at E intersects the tangents PA and PB:
- Let CE be the length of the tangent from C to E, and DE be the length of the tangent from D to E.
- By the property of tangents from a point to a circle, we have:
\( CE = CA \quad \text{(let's denote this as equation 1)} \)
\( DE = DB \quad \text{(let's denote this as equation 2)} \)

Step 5: Find the Perimeter of Triangle PCD
The perimeter of triangle PCD is given by:
\( \text{Perimeter} = PC + PD + CD \)
Using the tangent properties:
- We can express CD as:
\( CD = CE + DE \)
Substituting the values from equations 1 and 2:
\( CD = CA + DB \)
Now substituting back into the perimeter formula:
\( \text{Perimeter} = PC + PD + (CA + DB) \)
Since \(PC = PA\) and \(PD = PB\):
\( \text{Perimeter} = PA + PB + (CA + DB) \)
Substituting the known values:
\( \text{Perimeter} = 10 + 10 + (CA + DB) \)
Since \(CA = CE\) and \(DB = DE\) are also equal to the lengths of the tangents from points C and D to the circle:
\( \text{Perimeter} = 10 + 10 + 10 + 10 = 20 \text{ cm} \)

Final Answer
The perimeter of triangle PCD is:
\( \text{Perimeter} = 20 \text{ cm} \)