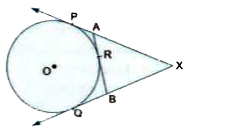
In the given figure, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA+AR=XB+BR.

We know that the lengths of tangents drawn from a exterior point to a circle are equal.
∴XP=XQ, ………(i)[tangents from X]
AP=AR, ………(ii) [tangents from A]
BR=BQ. ………..(iii) [tangents from B]
Now, XP=XQ⇒XA+AP=XB+BQ
⇒XA+AR=XB+BR [using (ii) and (iii)].
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A
16 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B
15 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
In Fig , XP and XQ are two tangents to the circle with centre O , drawn from an external point X . ARB is another tangent, touching the circle at R . Prove that XA + AR = XB + BR.
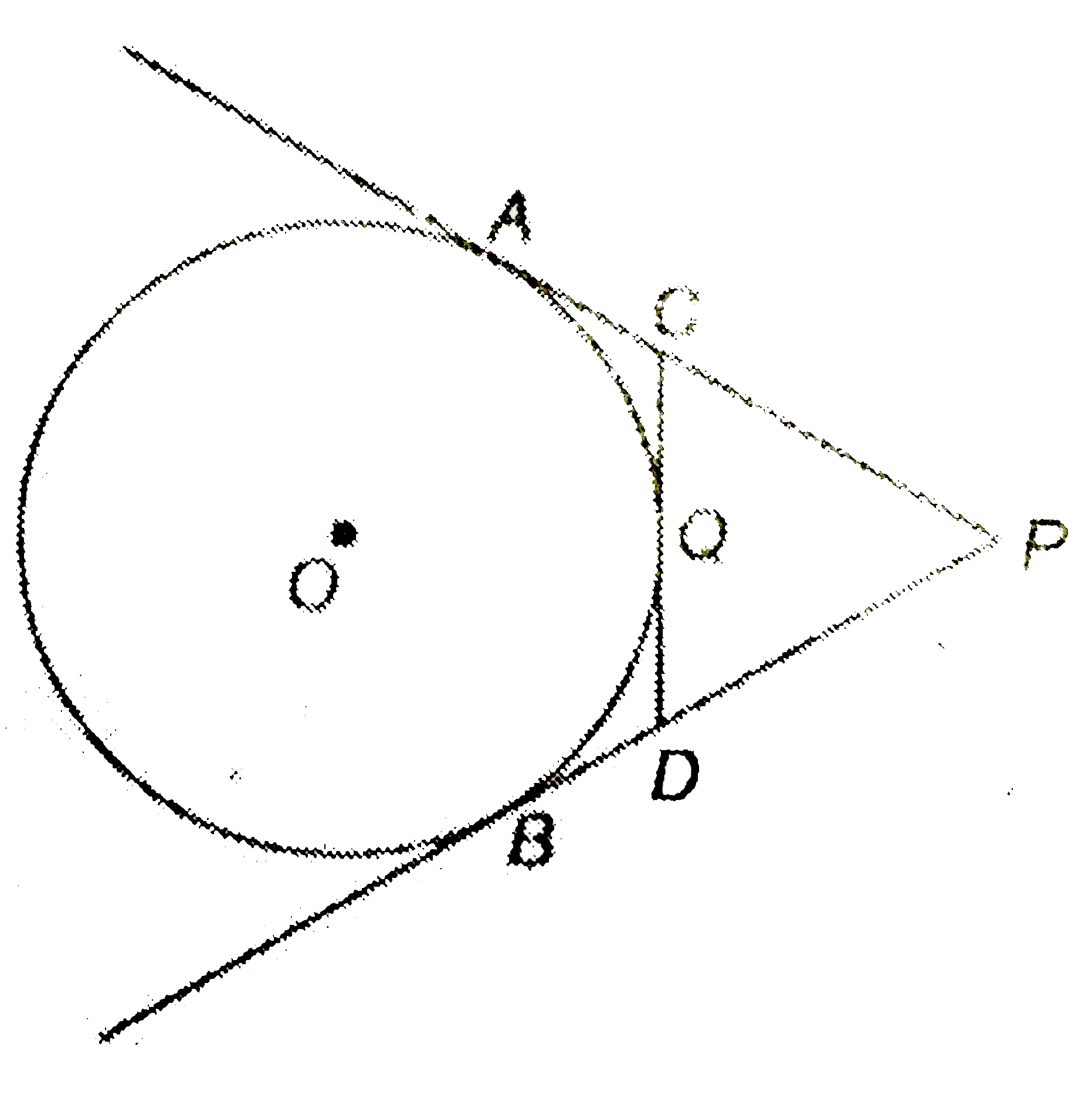
View SolutionIn the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA =12 cm, QC=3cm, then find PC+PD.
View Solution
Knowledge Check
Two tangents PA and PB are drawn to a circle with centre O from an external point P. If ∠OAB=30∘, then ∠APB is:
केंद्र O वाले वृत्त पर एक बाहरी बिंदु P से दो स्पर्श रेखाएँ PA तथा PB खींची जाती हैं | यदि ∠OAB=30∘ है, तो ∠APB का मान क्या होगा ?A15∘B30∘C120∘D60∘
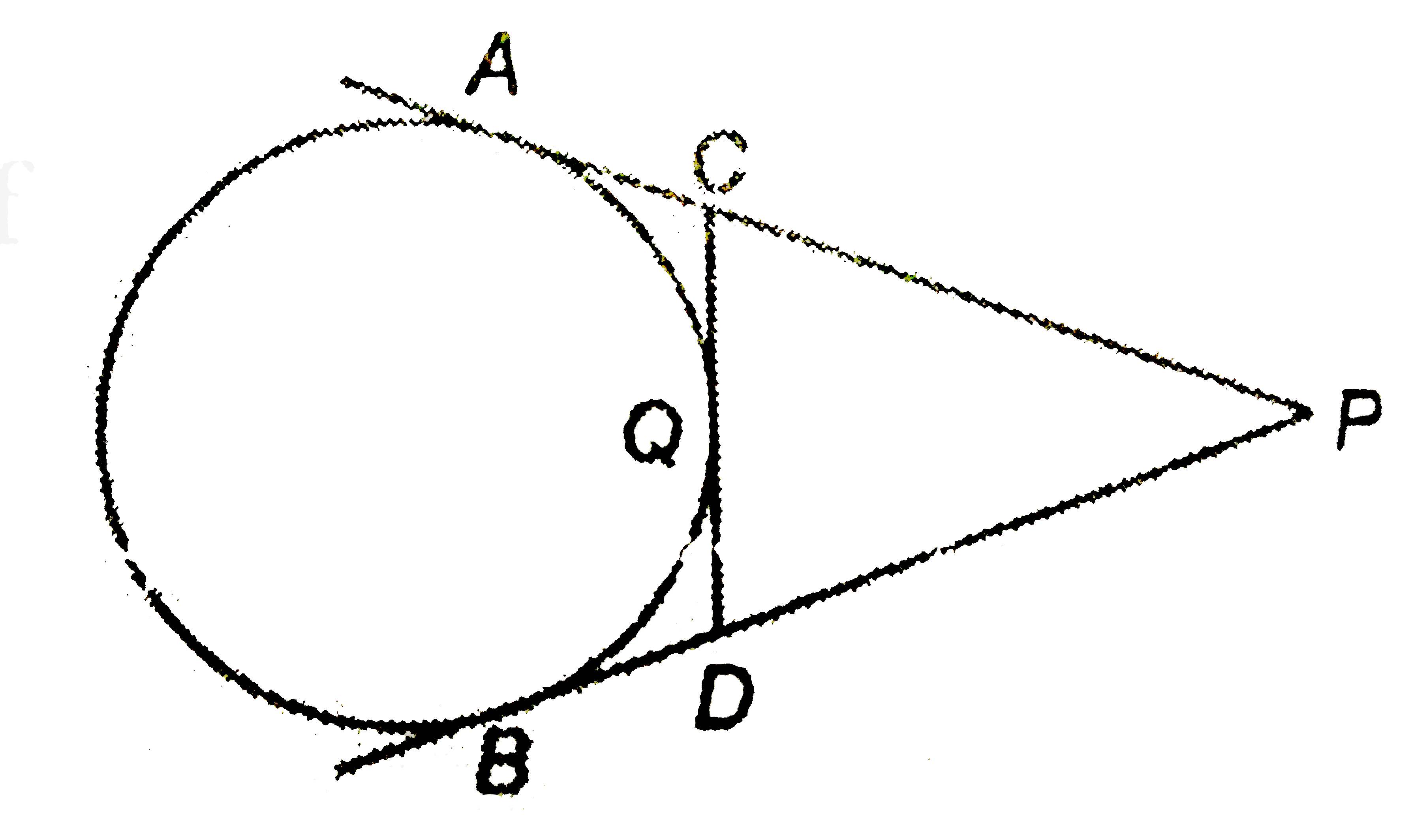
In the given figure PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB=10cm and CQ=2cm. What is the length of PC?
View SolutionProve that the length of the tangent drawn from an external point to a circle are equal. Using the above, do the following: TP and TQ are tangents from T to the circle with circle O and R in any point on the circle. If AB is a tangent to the circle at R, prove that TA + AR =TB +BR.

View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre C from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionPA and PB are tangents to the circle with centre O from an external point P, touching the circle at A and B respectively. Show that the quadrilateral AOBP is cyclic.
View SolutionIn Figure, XPandXQ are tangents from X to the circle with centre O.R is a point on the circle. Prove that, XA+AR=XB+BR
View SolutionCP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm, BC = 7cm, Then the length BR is :
View SolutionIn Figure 4, PQ and PR are tangents drawn to a circle with centre O from an external point P. If ∠PRQ=70∘, then find ∠QPRand∠OQR
View Solution
