In the given figure, XY || QR, PQ/XQ=7/3 and PR = 6.3 cm, find YR
The correct Answer is:2.7 cm
To solve the problem, we will follow these steps:
1. Understand the Given Information: We have two parallel lines XY and QR, and we know the ratio of segments PQ and XQ, which is given as PQXQ=73. We also know the length of segment PR, which is 6.3 cm. We need to find the length of segment YR.
2. Assign Variables: Let's denote the length of YR as x.
3. Apply Thales' Theorem: According to Thales' theorem, if two lines are parallel, then the ratios of the segments created by those lines are equal. Therefore, we can set up the equation:
PQXQ=PRYR
Substituting the known values, we have:
73=6.3x
4. Cross-Multiply to Solve for x: We can cross-multiply to solve for x:
7x=3×6.3
5. Calculate the Right Side: Now, calculate 3×6.3:
3×6.3=18.9
So, we have:
7x=18.9
6. Divide by 7: To find x, divide both sides by 7:
x=18.97
7. Perform the Division: Now, calculate 18.97:
x=2.7
8. Conclusion: Therefore, the length of YR is 2.7 cm.
Final Answer:
YR = 2.7 cm
---
PQXQ=PRYR
Substituting the known values, we have:
73=6.3x
7x=3×6.3
3×6.3=18.9
So, we have:
7x=18.9
x=18.97
x=2.7
YR = 2.7 cm
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (D)
8 Videos
- MATRICESBOOK - ICSECHAPTER - MATRICESEXERCISE - Exercise 9D
25 Videos
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
Similar Questions
In the given figure if PQ||YZ. Find XQ.

View SolutionIn the given figure, DE||BC and ADDB=23if AE=3.7 cm , find EC.

View SolutionIn the given figure, if AC=3cm and CB=6cm, find the length of CR.
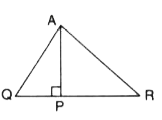
View SolutionIn the given figure , PR>PQ
Prove that : AR>AQ
View SolutionIn the given figure, PQ = 24 cm PR = 7 cm and O is the centre of the circle. Find the area of the shaded region. (Use π=3.14)

View SolutionIn the given figure, PQ//AB, CQ = 4.8 cm QB = 3.6 cm and AB = 6-3 cm. Find :

PQ
View SolutionIn the given figure, PQ//AB, CQ = 4.8 cm QB = 3.6 cm and AB = 6-3 cm. Find :

CPPA
View SolutionIn the given figure , ∠QPR=90∘ QR = 26 cm PM = 6cm, MR = 8cm and ∠PMR=90∘ . Find the area of triangle PQR.

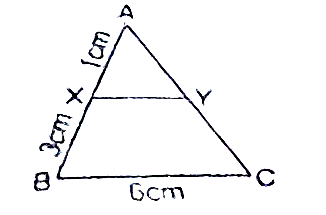
View SolutionIn the given figure , if XY||BC, find the length of XY.
View SolutionIn the given figure, AP = 8 cm, BP = 22 cm, AQ = 12 cm and QC = 8 cm

If PQ = 14 cm, find BC.
View Solution
