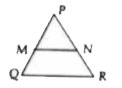
In the given if PM = PN and PM2=QM×NR, then which of the following is true ?

ΔPQM~ΔRPN
ΔPQM~ΔPRN
ΔPQM~ΔPNR
ΔPQM~ΔNRP
The correct Answer is:A
Topper's Solved these Questions
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (ASSERTION AND REASON BASED QUESTIONS)
5 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SHARES AND DIVIDENDSBOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )
20 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(E)
61 Videos
Similar Questions
In the given figure PM.PR=PN.PQ and is such that 4PM=3PQ. If area of ΔPQR is 32cm2, then area of quadrilateral MNRQ is
View SolutionIn each of the following letter series, some of the letters are missing which are give in that order as one of the alternatives below it. choose the correct alternative.
__op__mo__n__ __pnmop__
1) mnpmon
2)mpnmop
3) mnompn
4) mnpomn
5) None of these
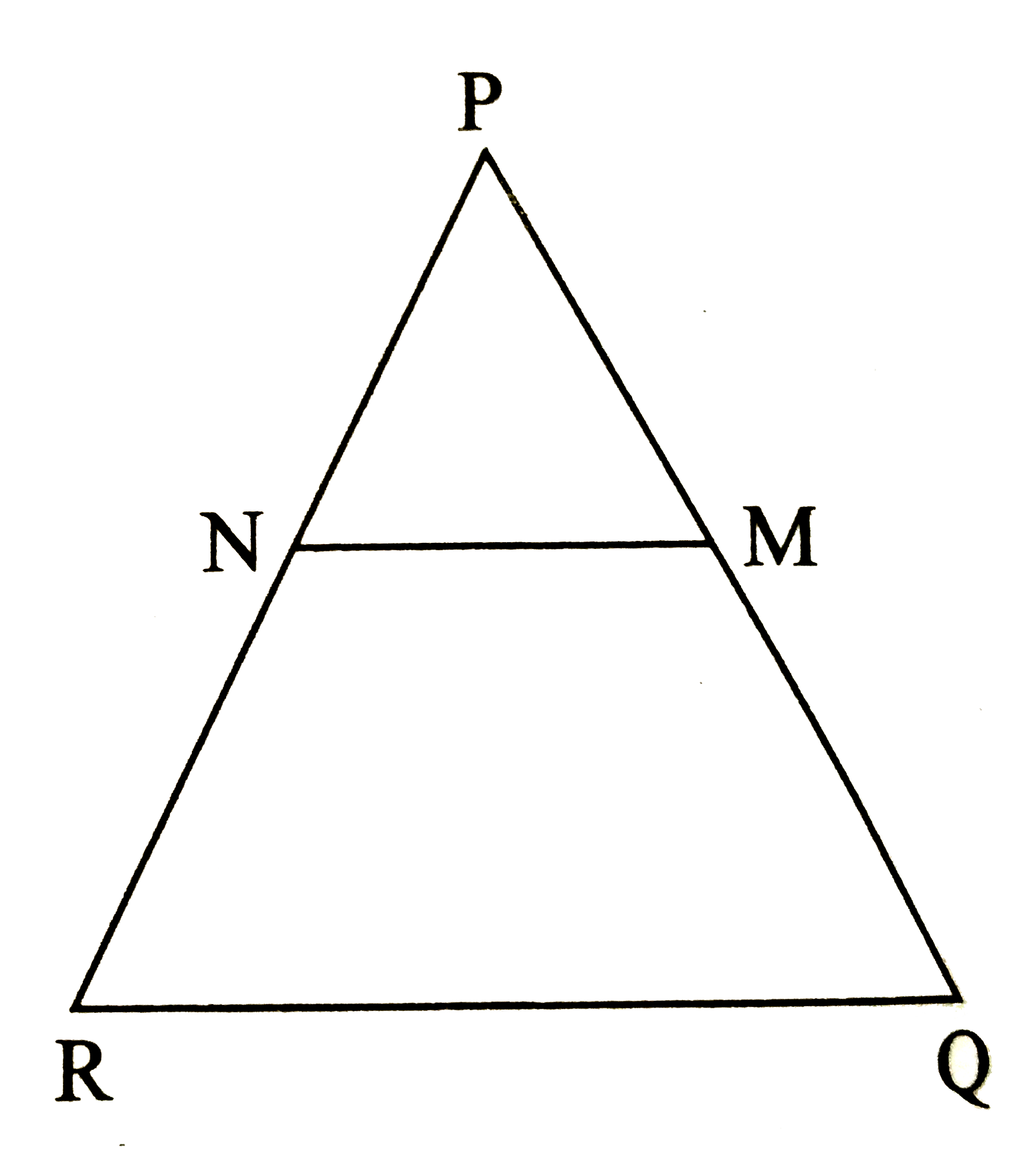
View SolutionIn ΔPQR, PM=15, MQ=10, PN=12 and NR=8. State whether line NM is parallel to side RQ or not. Give reason.
View SolutionIn Figure, prove that PM=PN= root 3 × a
View SolutionIn the given figure, seg PM is a median of ΔPQR.PM=9andPQ2+PR2=290, then find QR.

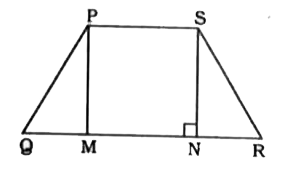
View SolutionIn the given figure, PQRS is a trapezium in which PM∣∣NS=9cm,PS=12cm,QM=NRandNR=SN. What is the area (in cm2) of trapezium?
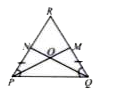
View SolutionIn the figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR such that QM = PN. Prove that OP=OQ, where O is the point of intersection of PM and QN.
View SolutionIn the given figure, Q is the centre of the circle and PM ,PN are tangent segments to the circle. If ∠MPN=50∘ find ∠MQN.
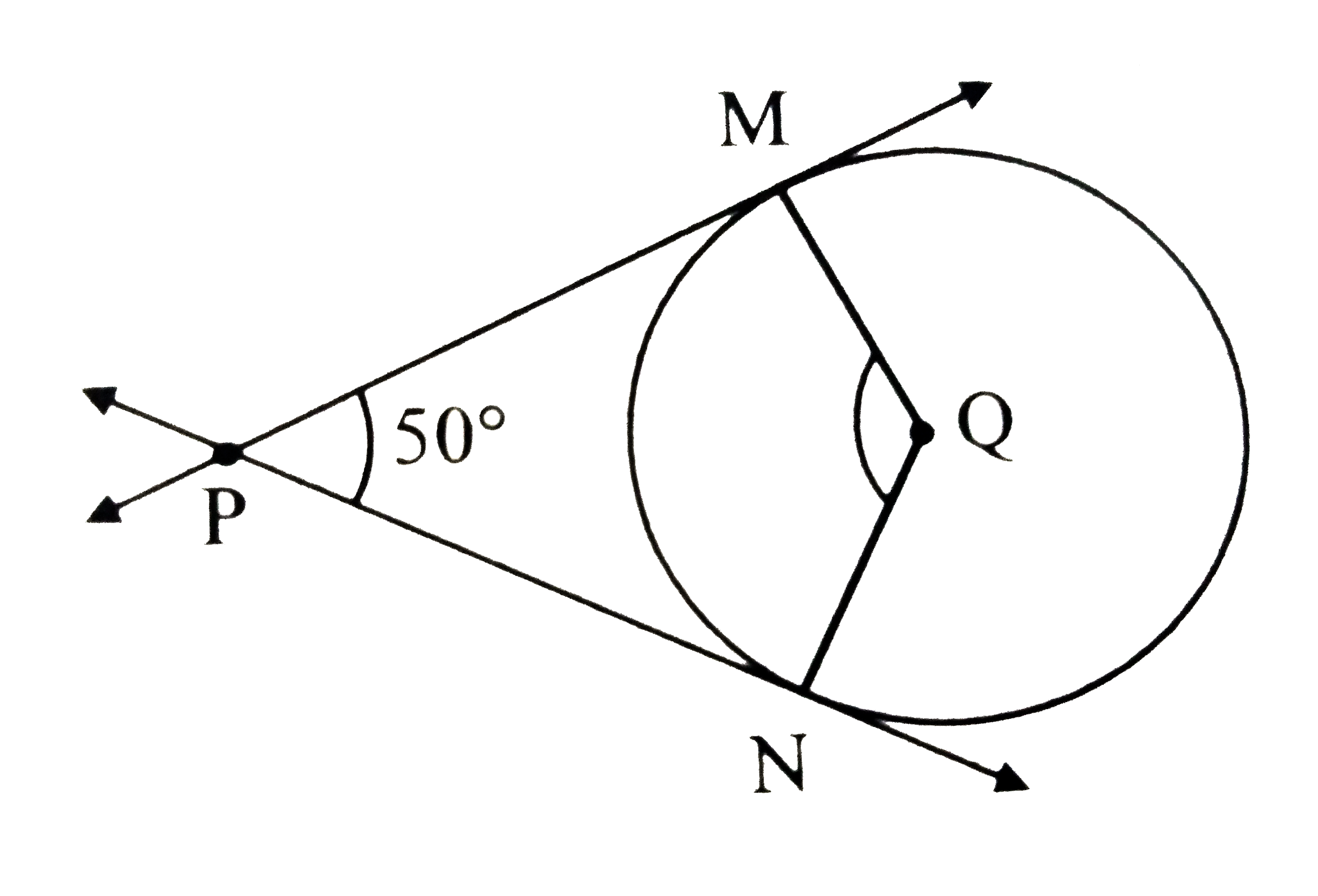
View SolutionIt is between 3 P.M. and 4 P.M. and the distance between the hour and the minute hand of clock is 18 minute spaces. What time does the clock show? (a) 3.12 P.M. (b) 3.27 P.M. (c) 3.31 P.M. (d) 3.36 P.M.
View SolutionIn the figrure, Q is the centre of the circle and PM and PN are tangent segments to the circle. If ∠MPN=40∘, find ∠MQN
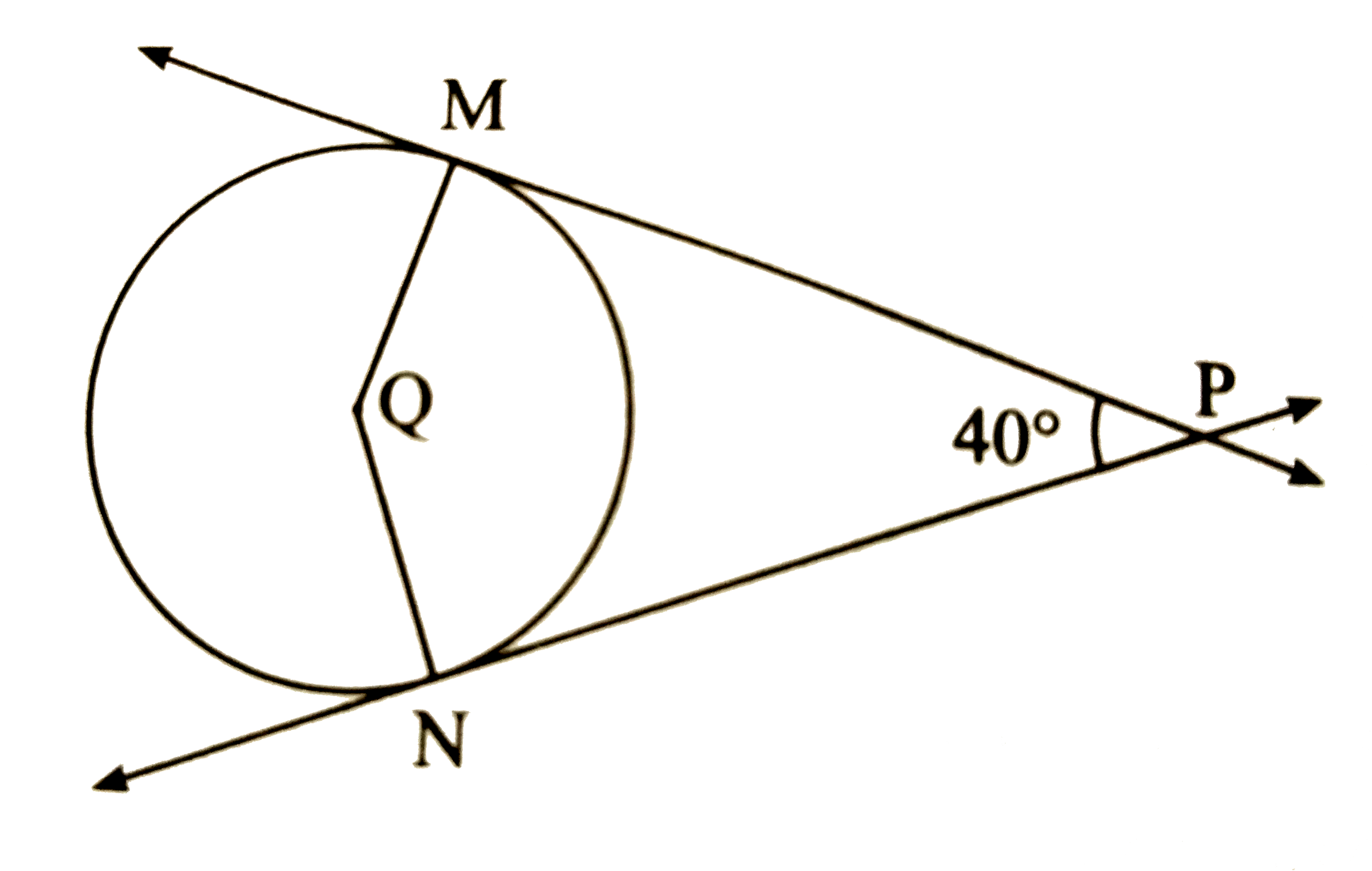
View Solution
