In the isosceles triangle ABC,AB=AC, if a circle is drawn with the side AB as diamter then the circle intersects the side BC at the point D. When BD=4 cm , find the the length of CD.Solution in Bengali
Let O is the mid-point of AB. Circle drawn with centre at O intersect the side BC at the point D. Let us join A,D. then ∠ADB is a semi-circular angle.
∴∠ADB=90∘,∴∠ADC=90∘
Now, in ΔABDandΔACD , we have AB=AC∠ABD=∠ACDand∠ADB=a∠ADC.
∴ΔABD≅ΔACD [ by the A-A-S condition of congruency]
∴Bd=CD[∴ similar side os congruent triangle]
But BD= 4 cm (Given) ∴CD=4cm

Topper's Solved these Questions
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.1 (Very Short-Answer Type Questions) MCQs
4 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.1 (True or False)
2 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs
5 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
Similar Questions
Area of a circle is 5544square meter ,then calculated the radius of the circle.
View SolutionThe front angle produced by an are of the circle is called the central angle.
View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionTwo circles are drawn with sides AB,AC of a triangle ABC as diameters. The circles intersect at a point D. Prove that D lies on BC.
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base. Given: A ABC in which AB=AC and a circle is drawn by taking AB as diameter which intersects the side BC of triangle at D To Prove: BD=DC Construction : Join AD
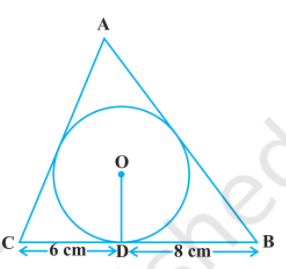
View Solution4cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC (जिनमें स्पर्श बिंदु D द्वारा BC विभाजित है) की लंबाइयाँ क्रमश : 8cm और 6cm हैं। भुजाएँ AB और AC ज्ञात कीजिए।
View Solution4 सेमी त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींची गया है कि रेखाखंड BD और DC (जिनमे स्पर्श बिन्दु D द्रारा BC विभाजित है ), की लम्बइया क्रमशः 8 सेमी और 6 सेमी है। भुजाएँ AB और AC ज्ञात कीजिए।
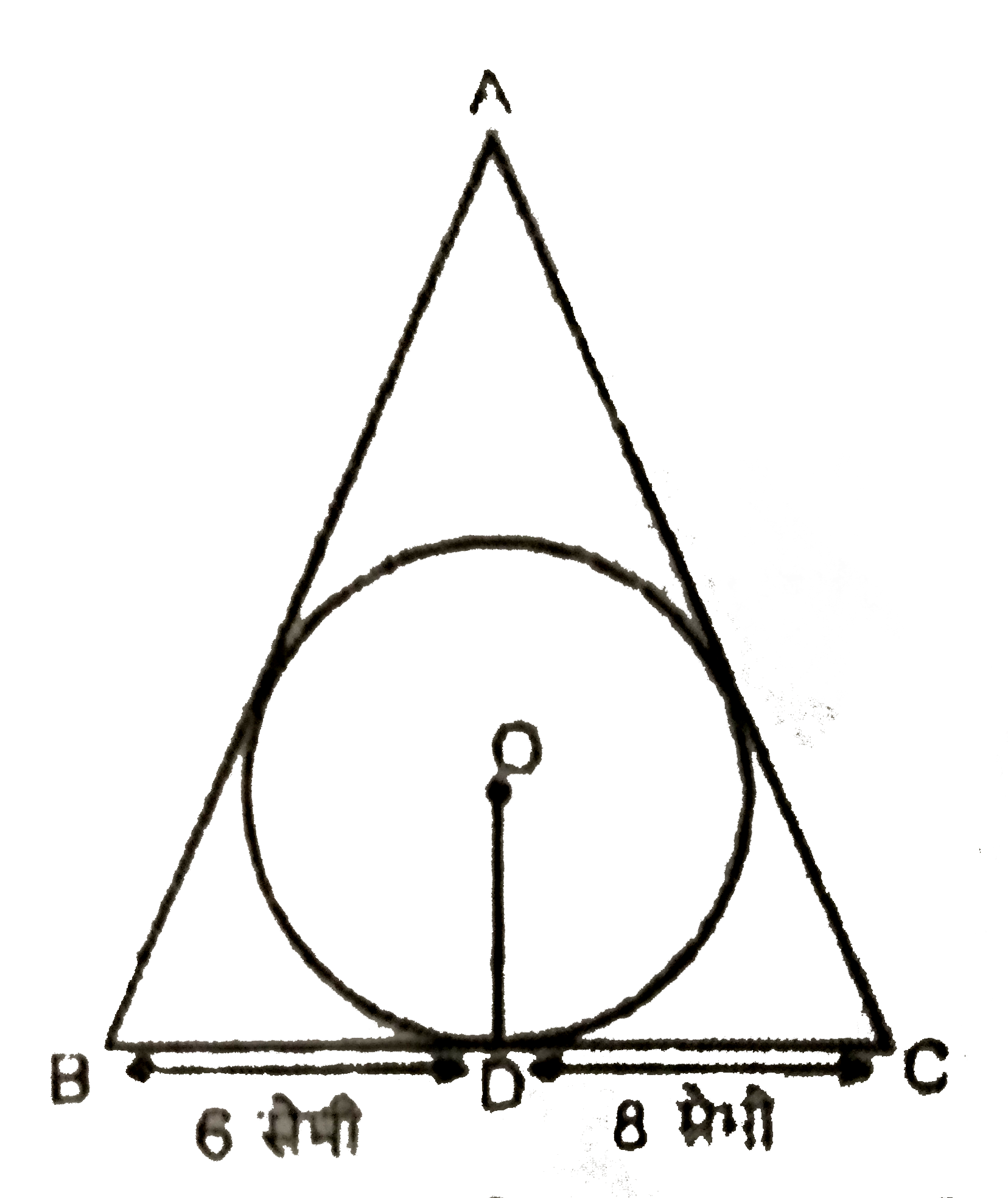
View Solution4 सेंमी त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया कि रेखाखण्ड BD और DC, जिनमें स्पर्श बिन्दु D द्वारा BC विभाजित है, की लम्बाईयाँ क्रमशः 8 सेमी और 6 सेमी हैं। यदि त्रिभुज ABC का क्षेत्रफल 84 सेमी2 हो, तो त्रिभुज की भुजाएँ AB तथा AC ज्ञात कीजिए ।
सिद्ध कीजिए कि किसी वृत्त के परिगत समातर चतुर्भुज, एक समचतुर्भुज होता है।
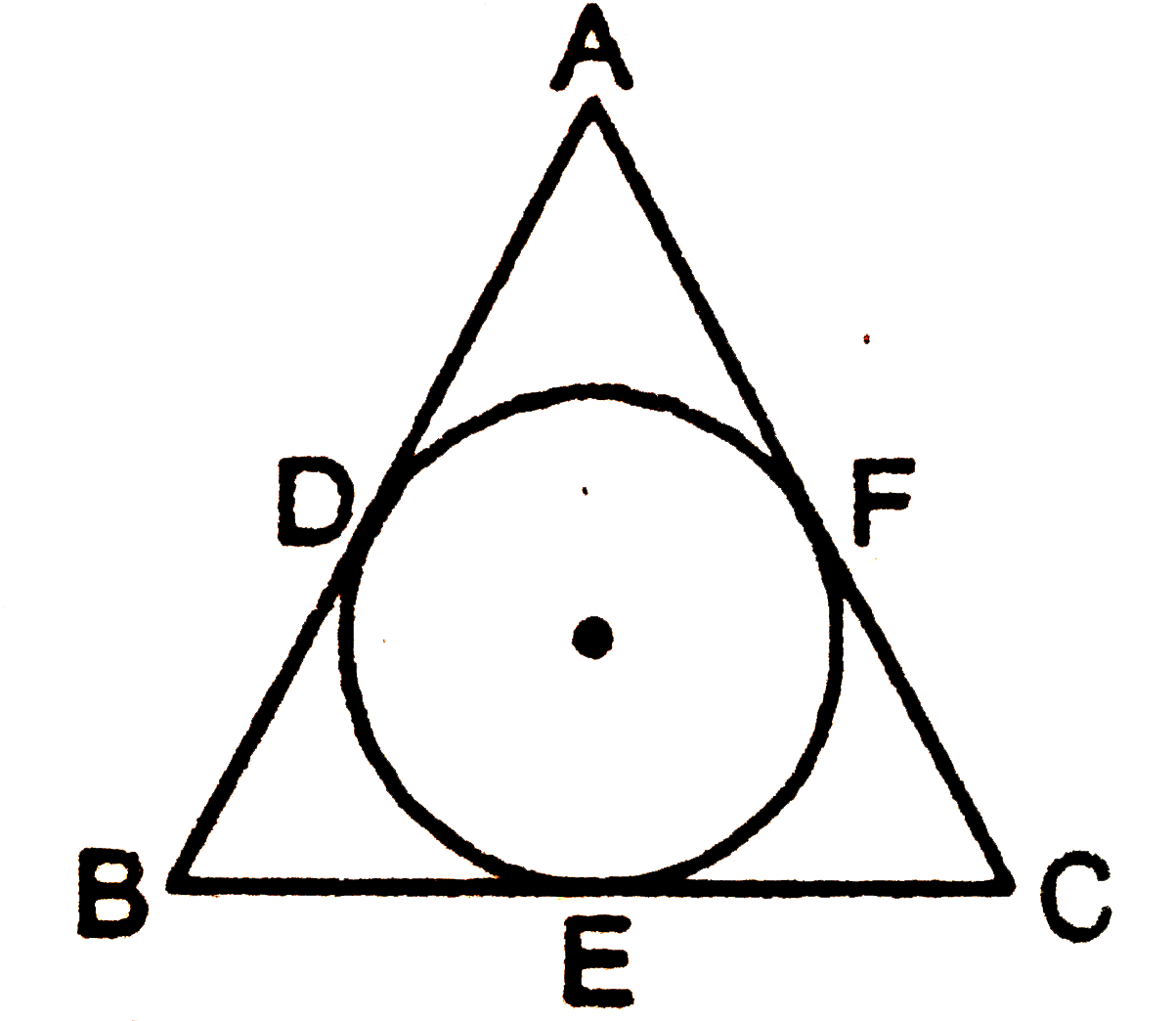
View Solutionत्रिभुज ABC के अंदर एक वृत्त है जो भुजा AB , BC और AC को क्रमशः बिंदु D , E और F पर स्पर्श करती है। अगर AB = 12 सेमी, BC = 8 सेमी और AC = 10 सेमी हो तो AD , BE और CF की लम्बाई ज्ञात करें।
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजा AC पर बिंदु D इस प्रकार है की BC2=AC×CD|यदि AB =AD हो तो सिद्ध करो की BD =BC
View SolutionΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB=AC त्रिभुज के अन्दर एक वृत्त इस प्रकार खींचा गया है कि यह भुजा AB को E पर, BC को D तथा AC कोF पर स्पर्श करती है। दिखाएँ कि D भुजा BC का माध्य बिन्दु है।
View SolutionA triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
View SolutionABC একটি সমদ্বিবাহু ত্রিভুজ যার AB=AC , BC -এর যে পার্শ্বে △ABC অবস্থিত, সেই পার্শ্বেই △DBC এমনভাবে অঙ্কন করা হলো যাতে ∠BAC=2∠BDC হয়। প্রমান করি যে, A -কে কেন্দ্র করে AB ব্যাসার্ধ নিয়ে যে বৃত্ত অঙ্কন করা হবে তা D বিন্দু ওই বৃত্তের উপর অবস্থিত হবে ।
View Solution