In the picture below, two lines are drawn from the top vertex of a triangle to the bottom side:
Prove that the ratio in which these lines divide the length of the bottom side is equal to the ratio of the area of the three smaller triangles in the picture.Solution in Malayalam
Step by step video & image solution for In the picture below, two lines are drawn from the top vertex of a triangle to the bottom side:Prove that the ratio in which these lines divide the length of the bottom side is equal to the ratio of the area of the three smaller triangles in the picture. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Prove that the.circumcentre of an equilateral triangle is the same as its centroid.
i) Calculate the length of a side. of an equilateral triangle with vertices on a circle of diameter 1 ceritimetre.
ii). Calculate the perimeter of such a triạngle.
View Solution'If a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionIf a line through one vertex of a triangle divides the opposite sides in the Ratio of other two sides; then the line bisects the angle at the vertex.
View SolutionProve that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
View SolutionIf a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionProve that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
View SolutionIf a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points. Prove that the other two sides are divided in the same ratio.
View SolutionIf a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionIf a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionIf a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionProve that if a line is drawn parallel to one side of a triangle to intersect its other two sides, then these two sides are divided in the same ratio.
View SolutionIf a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. Prove it.
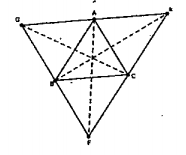
View SolutionIn the picture below, the lines parallel to each side of the blue triangle through the opposite vertex are drawn to make the big triangle.
How many triangles in the picture have the same area as that of the blue triangle.
View SolutionIn the picture below, the top vertex of a triangle is joined to the midpoint of the bottom side of the triangle and then the midpoint of this line is joined to the other two vertices. Prove that the areas of all four triangles obtained thus are equal to a fourth of the area of the whole triangle.
View SolutionIn the picture below, the top vertex of a triangle is joined to the midpoint of the opposite side and then the point dividing this line in the ratio 2:1 is joined to the other two vertices. Prove that the areas of all three triangles in the picture on the right are equal to a third of the area of the whole triangle
View SolutionIn this picture the horizontal lines at the top and bottom are parallel. Prove that the yellow and red triangles are of the same area.
View Solution
