In triangle ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.
To solve the problem, we will follow these steps:
Step 1: Understand the Given Information
We have triangle ABC with D and E as midpoints of sides AB and AC, respectively. A line through E is drawn parallel to AB, meeting BC at point F.
Step 2: Use the Midpoint Theorem
According to the midpoint theorem, if a line segment connects the midpoints of two sides of a triangle, it is parallel to the third side and half its length.
1. Since D is the midpoint of AB, we have:
AD=DB=AB2=16 cm2=8 cm
2. Since E is the midpoint of AC, we have:
AE=EC=AC2=12 cm2=6 cm
Step 3: Establish Relationships Using the Midpoint Theorem
Since EF is drawn parallel to AB and E is the midpoint of AC, by the midpoint theorem, F must be the midpoint of BC.
1. Therefore:
BF=FC=BC2=18 cm2=9 cm
Step 4: Prove BDEF is a Parallelogram
To prove that BDEF is a parallelogram, we need to show that both pairs of opposite sides are equal and parallel.
1. We know:
- DE is parallel to BF (by the midpoint theorem)
- EF is parallel to AB (given)
2. Also, we have:
- DE = BF (since DE connects the midpoints of AB and AC)
- EF = BD (since EF is parallel to AB and both are equal)
Thus, we have:
- DE || BF and DE = BF
- EF || AB and EF = BD
Since both pairs of opposite sides are equal and parallel, BDEF is a parallelogram.
Step 5: Calculate the Perimeter of Parallelogram BDEF
The perimeter of a parallelogram is given by the formula:
Perimeter=2×(BF+EF)
Substituting the values we found:
- BF=9 cm
- EF=8 cm
Thus, the perimeter is:
Perimeter=2×(9 cm+8 cm)=2×17 cm=34 cm
Final Answer
The perimeter of the parallelogram BDEF is 34 cm.
---
We have triangle ABC with D and E as midpoints of sides AB and AC, respectively. A line through E is drawn parallel to AB, meeting BC at point F.
According to the midpoint theorem, if a line segment connects the midpoints of two sides of a triangle, it is parallel to the third side and half its length.
AD=DB=AB2=16 cm2=8 cm
AE=EC=AC2=12 cm2=6 cm
Since EF is drawn parallel to AB and E is the midpoint of AC, by the midpoint theorem, F must be the midpoint of BC.
BF=FC=BC2=18 cm2=9 cm
To prove that BDEF is a parallelogram, we need to show that both pairs of opposite sides are equal and parallel.
- DE is parallel to BF (by the midpoint theorem)
- EF is parallel to AB (given)
- DE = BF (since DE connects the midpoints of AB and AC)
- EF = BD (since EF is parallel to AB and both are equal)
- DE || BF and DE = BF
- EF || AB and EF = BD
The perimeter of a parallelogram is given by the formula:
Perimeter=2×(BF+EF)
- BF=9 cm
- EF=8 cm
Perimeter=2×(9 cm+8 cm)=2×17 cm=34 cm
The perimeter of the parallelogram BDEF is 34 cm.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)EXERCISE - EXERCISE 12(A)23videos
MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)
- BOOK - ICSECHAPTER - MENSURATION (PLANE FIGURE) EXERCISE - TOPIC-3 (4 Marks Questions)8videos
MENSURATION (PLANE FIGURE)
- BOOK - ICSECHAPTER - MID-POINT THEOREMEXERCISE - 4 MARKS QUESTION15videos
MID-POINT THEOREM
Similar Questions
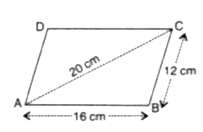
In parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
 View Solution
View SolutionIn triangle ABC, D and E are mid-points of sides AB and BC respectively. Also, F is a point in side AC so that DF is parallel to BC
(i) Prove that DBEF is a parallelogram.View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Prove that BDFE is a parallelogramView SolutionIn triangle ABC, D and E are mid-points of sides AB and BC respectively. Also, F is a point in side AC so that DF is parallel to BC
Find the perimeter of parallelogram DBEF, if AB = 10 cm, BC = 8.4 cm and AC = 12 cm.View SolutionIn triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
View SolutionIn ΔABC,D,E and F are mid-point of sides AB ,BC and AC respectively , Prove that AE and DF bisect each other.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD is perpendicular to EF.View SolutionIn triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find :
cos BView SolutionIn triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find :
sin CView Solution

