In triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
F is equidistant from AB and BC.
Step by step video & image solution for In triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of angleABC meets CD at E and AC at F. Prove that: F is equidistant from AB and BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CIRCLES)9videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (TANGENTS AND INTERSECTING CHORDS)10videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (SIMILARITY)10videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - BANKING (RECURRING DEPOSIT ACCOUNTS)EXERCISE - QUESTIONS7videos
BANKING (RECURRING DEPOSIT ACCOUNTS)
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )28videos
CIRCLES
Similar Questions
In triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
E is equidistant from A and BView SolutionThe given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that : F is equidistant from AB and AC.View SolutionConstruct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
View SolutionIn triangle ABC, AB > AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that : AB2+AC2=2AE2+2BE2
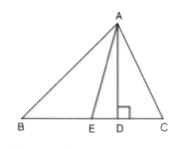 View Solution
View SolutionIn the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that :
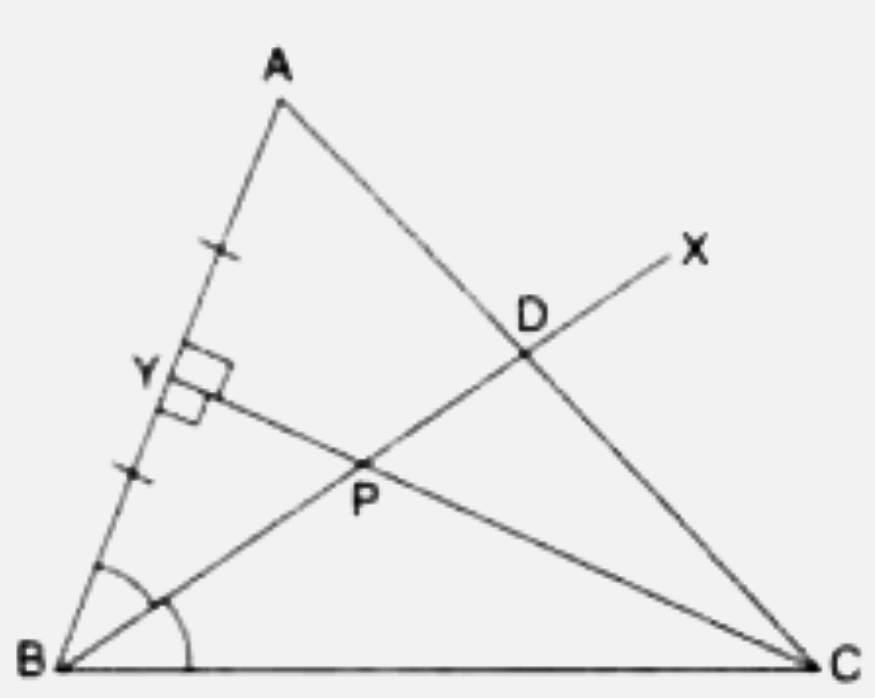
point D is equidistant from AB and BC.View SolutionIn the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that : point P is equidistant from A and B.
View SolutionIn a triangle ABC, D is a point on BC such that AD is the internal bisector of ∠A. Let ∠B=2∠C and CD = AB. Then ∠A is
View SolutionIn triangle ABC, AB=AC and BD is perpendicular to AC. Prove that : BD2−CD2=2CD×AD
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View SolutionIn triangle ABC, D is mid-point of AB and P is any point on BC. If CQ parallel to PD meets AB at Q, prove that: 2× area (ΔBPQ)= area (ΔABC)
View Solution

