In triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that BP=PMandCQ=QN. Prove that :
A is the mid-point of MN.
The correct Answer is:AN=AM
Step by step video, text & image solution for In triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that BP=PM and CQ=QN. Prove that : A is the mid-point of MN. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MID-POINT THEOREMEXERCISE - 4 MARKS QUESTION15videos
MID-POINT THEOREM
- BOOK - ICSECHAPTER - MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)EXERCISE - EXERCISE 12(B)23videos
MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)
- BOOK - ICSECHAPTER - PYTHAGORAS THEORAMEXERCISE - QUESTIONS9videos
PYTHAGORAS THEORAM
Similar Questions
In triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that BP = PM and CQ = QN. Prove that:
M, A and N are collinear.View SolutionIn triangle ABC, BE ad CF are median M is a point on BE produced such that BE=EM and N is point on CF produced such that CF=FN. Prove that
A is the mid-point of MNView SolutionIn a triangle ABC,D is the mid - point of BC, AD is produced upto E so that DE = AD.
Prove that :
AB=ECView SolutionIn triangle ABC, BE ad CF are median M is a point on BE produced such that BE=EM and N is point on CF produced such that CF=FN. Prove that
NAM is a straight lineView SolutionLet the area of a given triangle ABC be Δ. Points A1,B1,andC1 , are the mid points of the sides BC,CA and AB respectively. Point A2 is the mid point of CA1. Lines C1A1andAA2 meet the median BB1 points E and D respectively. If Δ1 be the area of the quadrilateral A1A2DE, using vectors or otherwise find the value of Δ1Δ
View SolutionA parallelogram ABCD has P the mid-point of DC and Q a midpoint of AC such that CQ=14AC.PQ produced meets BC at R. Prove that:
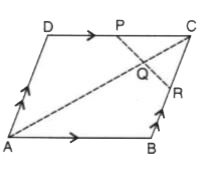
R is the mid-point of BCView SolutionIn trapezium ABCD, AB is parallel to DC. P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E. Prove that :
PQ is parallel to AB.View SolutionIn trapezium ABCD, AB is parallel to DC. P and Q are the mid-points of AD and BC respectively. BP product meets CD produced at point E. Prove that :
Point P bisects BE,View SolutionM and N are mid- point on sides QR and PQ respectively of △PQR, right-anggled at Q. Prove that :
PM2+RN2=5MN2.View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
area of BDEF is half the area of ΔABC.View Solution
