In a triangle ABC,D is the mid - point of BC, AD is produced upto E so that DE = AD.
Prove that :
AB=EC
The correct Answer is:AB=EC
To prove that AB=EC in triangle ABC where D is the midpoint of BC and AD is extended to E such that DE=AD, we can follow these steps:
1. Draw Triangle ABC:
- Begin by sketching triangle ABC with points A, B, and C.
2. Identify Midpoint D:
- Mark point D as the midpoint of side BC. This means BD=DC.
3. Extend AD to Point E:
- Extend line segment AD to point E such that DE=AD.
4. Label the Given Information:
- We know that DE=AD (given) and BD=DC (since D is the midpoint).
5. Identify Vertically Opposite Angles:
- Note that angles ∠ADB and ∠CDE are vertically opposite angles. Therefore, ∠ADB=∠CDE.
6. Form Triangles ABD and DEC:
- Consider triangles ABD and DEC.
7. Establish Congruence:
- We have the following:
- BD=DC (as D is the midpoint)
- AD=DE (given)
- ∠ADB=∠CDE (vertically opposite angles)
- By the Side-Angle-Side (SAS) congruence criterion, we can conclude that △ABD≅△DEC.
8. Apply CPCTC:
- Since the triangles are congruent, their corresponding parts are equal. Thus, we have AB=EC.
Conclusion:
We have proved that AB=EC.
- Begin by sketching triangle ABC with points A, B, and C.
- Mark point D as the midpoint of side BC. This means BD=DC.
- Extend line segment AD to point E such that DE=AD.
- We know that DE=AD (given) and BD=DC (since D is the midpoint).
- Note that angles ∠ADB and ∠CDE are vertically opposite angles. Therefore, ∠ADB=∠CDE.
- Consider triangles ABD and DEC.
- We have the following:
- BD=DC (as D is the midpoint)
- AD=DE (given)
- ∠ADB=∠CDE (vertically opposite angles)
- By the Side-Angle-Side (SAS) congruence criterion, we can conclude that △ABD≅△DEC.
- Since the triangles are congruent, their corresponding parts are equal. Thus, we have AB=EC.
We have proved that AB=EC.
Topper's Solved these Questions
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 3 MARKS QUESTIONS
11 Videos
- STATISTICS AND GRAPH WORK BOOK - ICSECHAPTER - STATISTICS AND GRAPH WORK EXERCISE - TOPIC - 2 (4 Marks Questions)
14 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
Similar Questions
In a triangle ABC, D is mid-point of BC, AD is produced upto E so that DE = AD. Prove that :
(i) ΔABDandΔECD are congruent.
(ii) AB = EC
(iii) AB is parallel to EC.
View SolutionIn a ΔABC,D in mid-point of BC, AD is produced upto E so that DE=AD, prove that :
(i) ΔABD and ΔECD are congruent (ii) AB=EC
(iii) AB is parallel to EC.
View SolutionIn a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE. Prove that : AE is parallel to BC.
View SolutionIn triangle ABC, AB > AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that : AB2+AC2=2AE2+2BE2
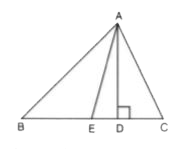
View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionAny point D is taken on the side BC of a ΔABC and AD is produced to E such that AD = DE , prove that area of ΔBCE= area of ΔABC,
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.

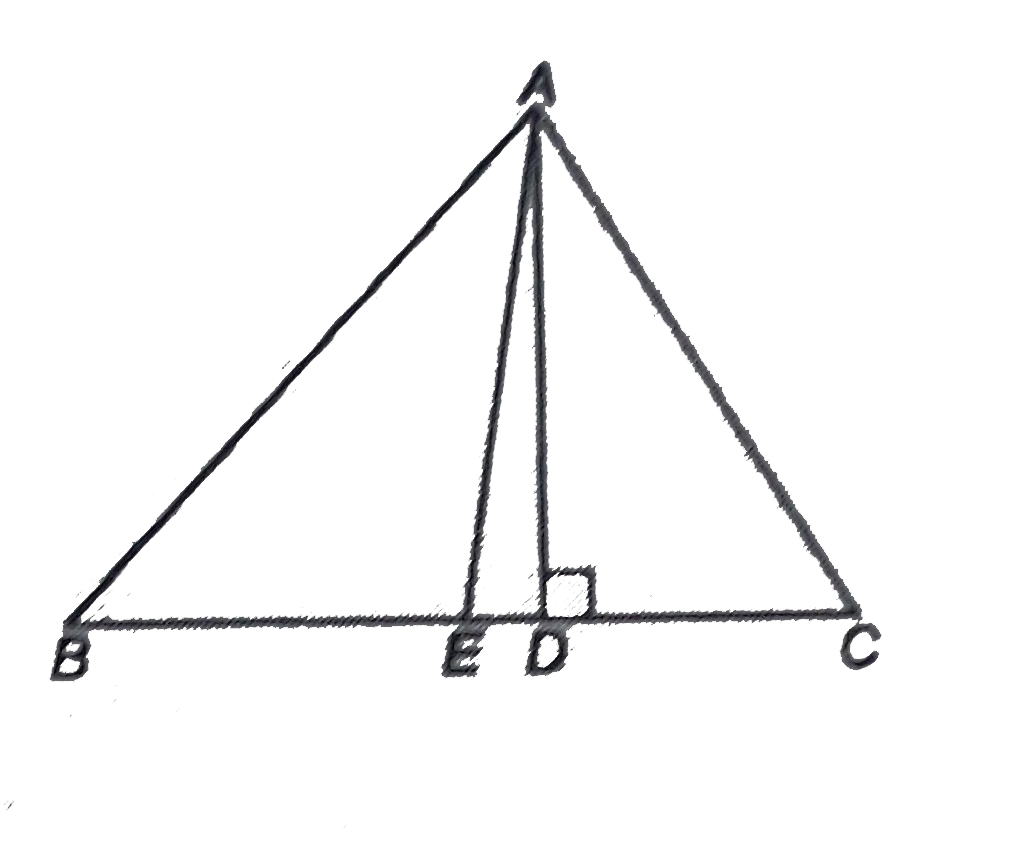
View SolutionThe given figure shows a triangle ABC, in which AB>AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that AB2−AC2=2BC×ED.
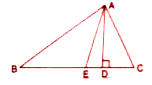
View SolutionThe given figure shows a triangle ABC, in which AB > AC. E is the mid-point of BC and AD is perpendicular to BC.
Prove that : AB2+AC2=2BE2+2AE2
View SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.
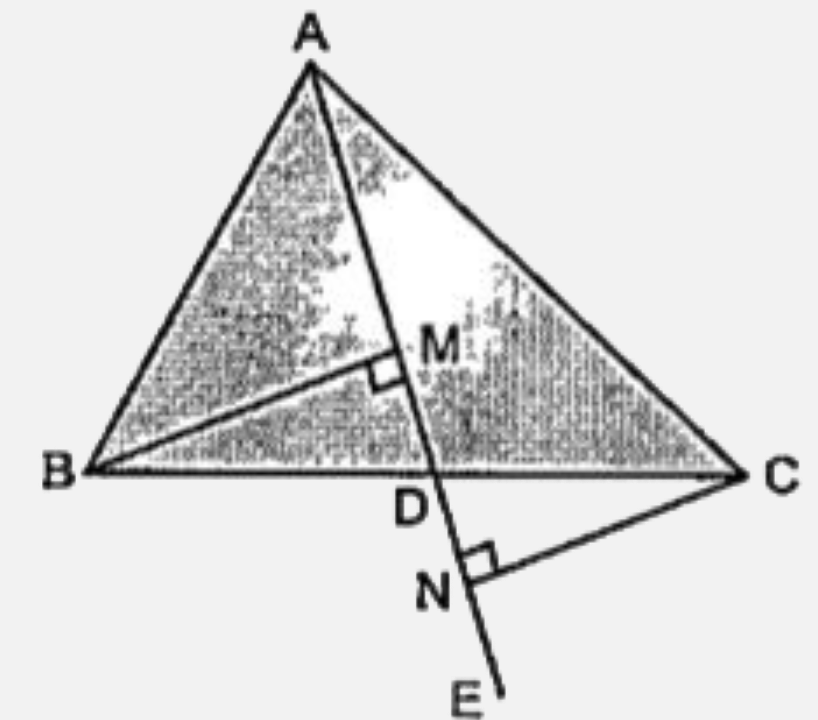
Prove that :
BM=CN
View Solution