In △ABC, it is given that D is the midpoint of BC, E is the midpoint of BD and O is the midpoint of AE. Then, ar(△BOE) = ?
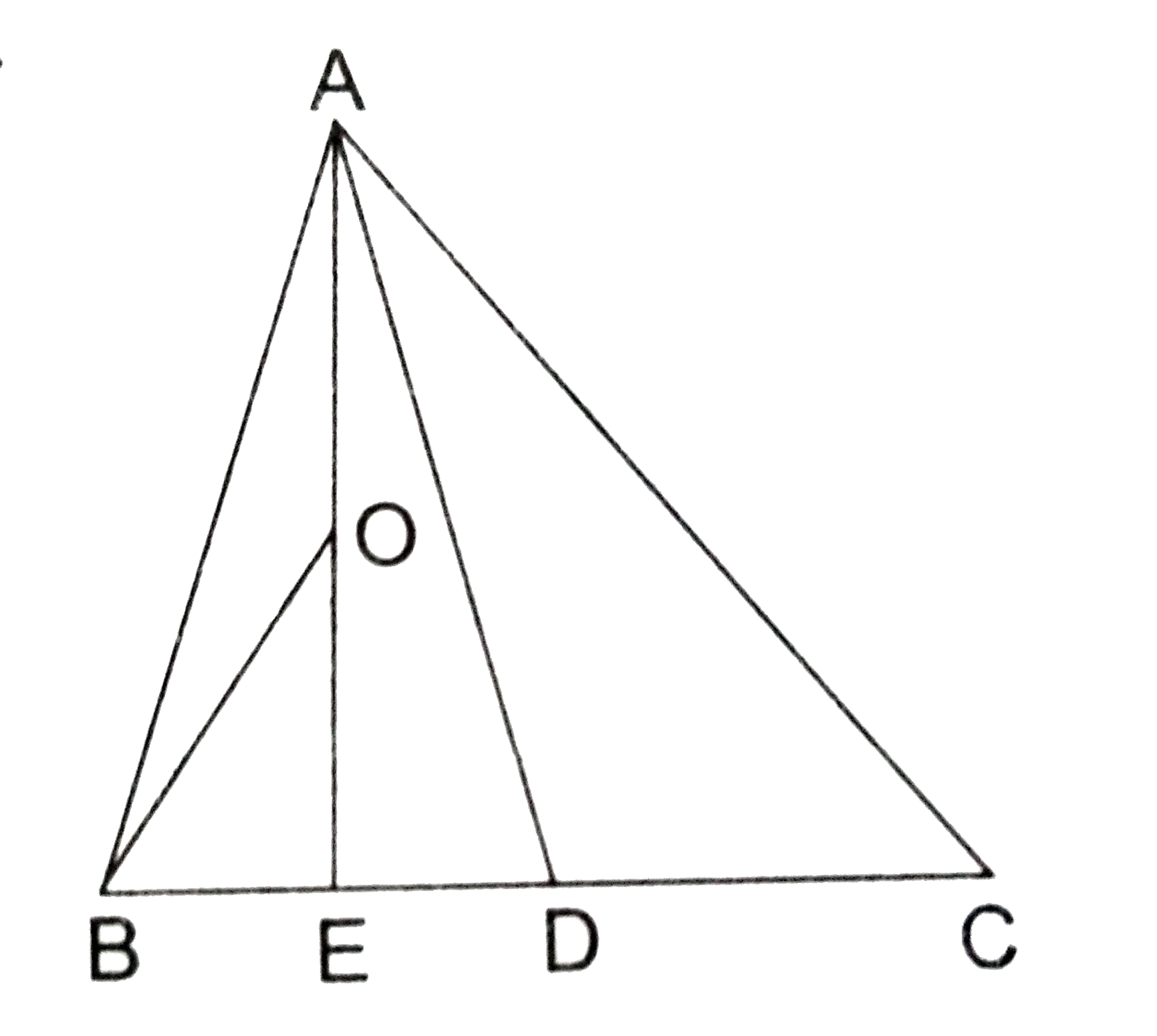
13ar(△ABC)
14ar(△ABC)
16ar(△ABC)
18ar(△ABC)
The correct Answer is:D
Median AD divides △ABC into two △ of equal area.
∴ar(△ABD)=12ar(△ABC).
Median AE divides △ABD into two △ of equal area.
∴ar(△ABE)=12ar(△ABD)=14ar(△ABC).
Median OB divides △ABE into two △ of equal area.
∴ar(△BOE)=12ar(△ABE)=18ar(△ABC).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
In △ABC, if D is the midpoint of BC and E is the midpoint of AD then ar(△BED) = ?
 A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)In triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of ΔABC is 96, the area of ΔAEF is
A16B24C32D36The area of △ABC is 88cm2. If D is the midpoint of BC and E is the midpoint of AB, then the area (in cm2) of △BDE is:
A44B22C11D5.5
In an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?

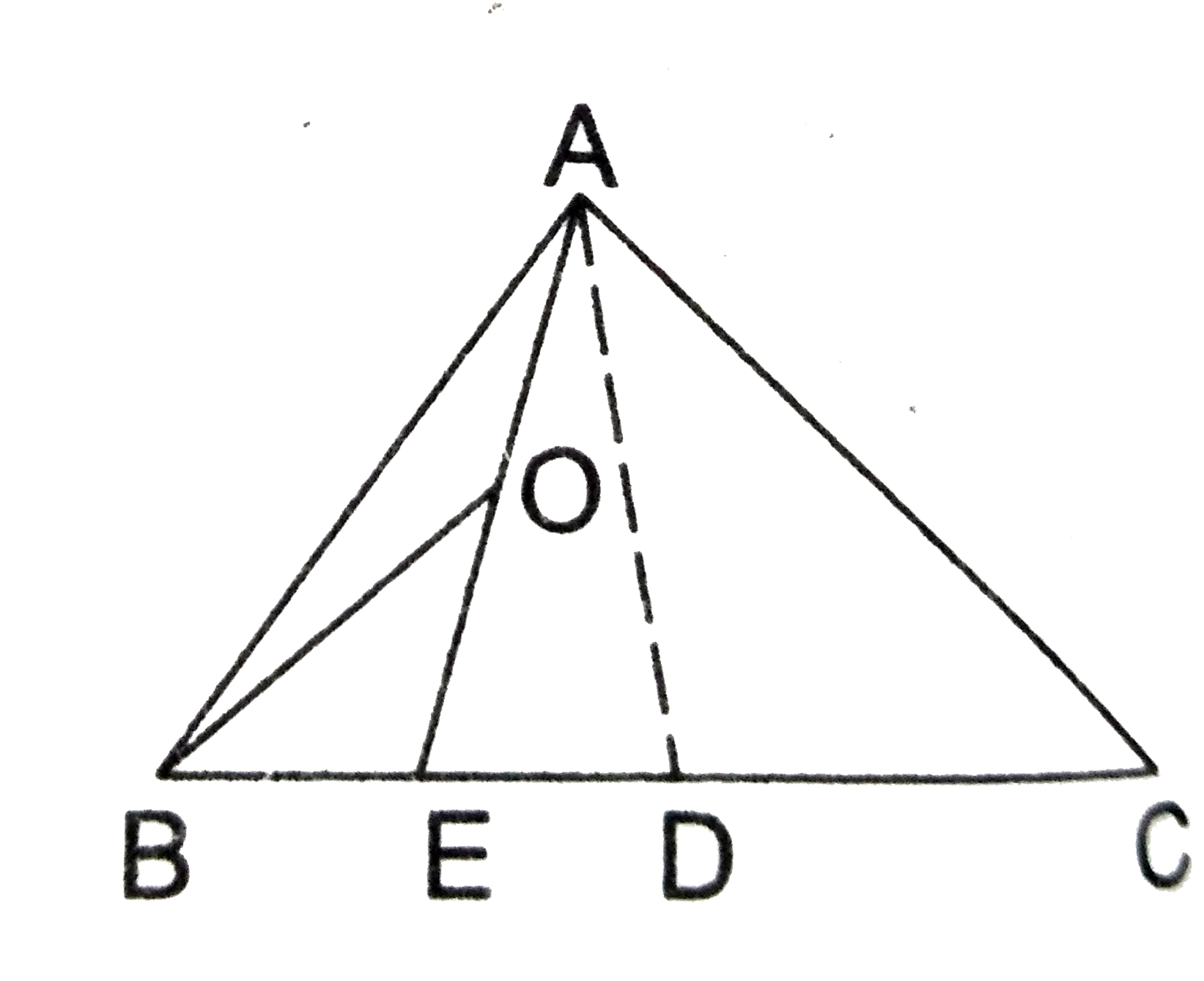
View SolutionD is the midpoint of side BC of △ABC and E is the midpoint of BD. If O is the midpoint of AE,
prove that ar(△BOE)=18ar(△ABC).
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

View SolutionIn an acute-angled triangle "ABC" ,let "D" be the foot of the altitude from "A" and "E" be the midpoint of "BC" .Let "F" be the midpoint of "AC" .Suppose ∠BAE=40∘. If ∠DAE=∠DFE ,then ∠ADF in degrees will be:
View SolutionIn ΔABC, D is the midpoint of side BC, E is mid point of AD, F is midpoint of BE and G is mid-point of FC. What part of the area of ΔABC is the area of ΔEFG?
View Solution

