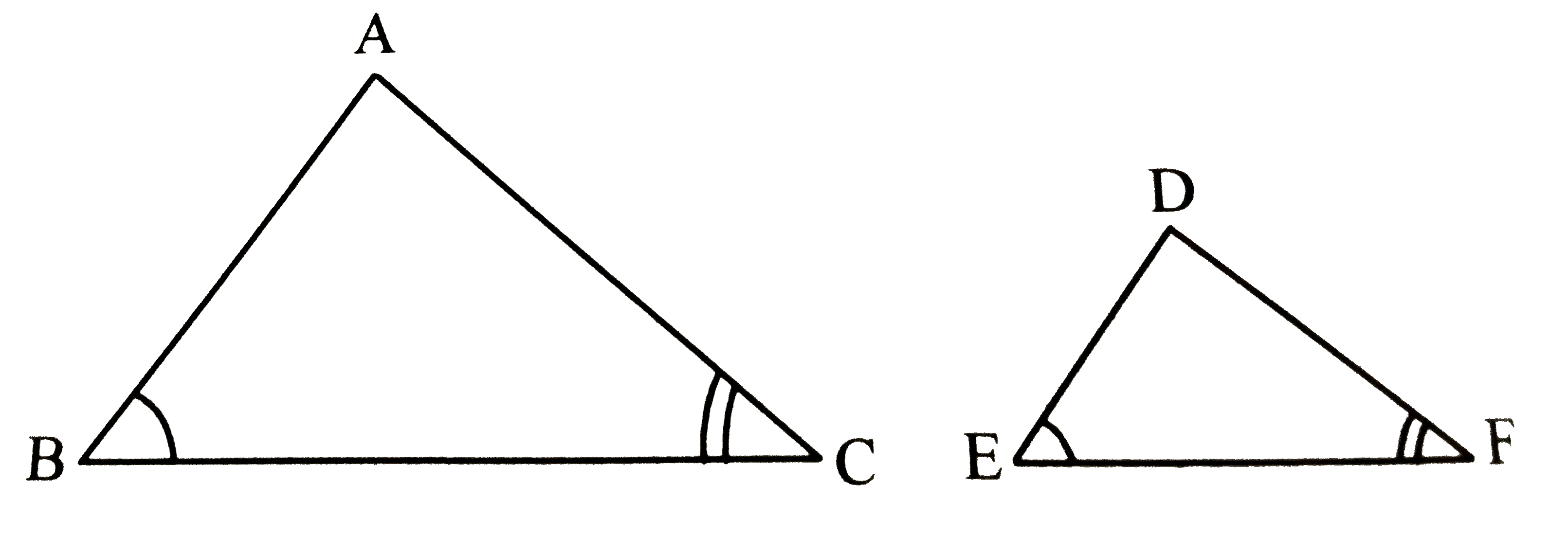
In two triangle ABC and DEF, if AB = BC , ∠B=∠E, DE=EF and BC = Ef , then which of the following statements is CORRECT ?
Triangles are congruent only .
Triangles are isosceles only .
Both triangles are congruent and isosceles
Both the triangles are neither congruent nor isosceles .
The correct Answer is:C
To solve the problem, we need to analyze the given information about triangles ABC and DEF step by step.
Step 1: Understand the Given Information
We are given:
- AB = BC (Two sides of triangle ABC are equal)
- ∠B = ∠E (Angle B in triangle ABC is equal to angle E in triangle DEF)
- DE = EF (Two sides of triangle DEF are equal)
- BC = EF (The side BC in triangle ABC is equal to the side EF in triangle DEF)
Step 2: Identify the Type of Triangles
Since AB = BC, triangle ABC is an isosceles triangle. Similarly, since DE = EF, triangle DEF is also an isosceles triangle.
Step 3: Analyze the Angles
We know that in triangle ABC:
- AB = BC implies that ∠A = ∠C (the angles opposite to the equal sides are equal).
In triangle DEF:
- DE = EF implies that ∠D = ∠F (the angles opposite to the equal sides are equal).
Step 4: Compare the Triangles
Now we have:
- ∠B = ∠E (given)
- ∠A = ∠C (from triangle ABC)
- ∠D = ∠F (from triangle DEF)
Step 5: Use the SAS Congruence Criterion
We can now apply the SAS (Side-Angle-Side) congruence criterion:
- AB = EF (given)
- ∠B = ∠E (given)
- BC = DE (since BC = EF and DE = EF, we can say BC = DE)
Thus, we have two sides and the included angle equal in both triangles:
- AB = EF
- ∠B = ∠E
- BC = DE
Conclusion
By the SAS criterion, triangle ABC is congruent to triangle DEF. Therefore, the correct statement is that both triangles are congruent and isosceles.
We are given:
- AB = BC (Two sides of triangle ABC are equal)
- ∠B = ∠E (Angle B in triangle ABC is equal to angle E in triangle DEF)
- DE = EF (Two sides of triangle DEF are equal)
- BC = EF (The side BC in triangle ABC is equal to the side EF in triangle DEF)
Since AB = BC, triangle ABC is an isosceles triangle. Similarly, since DE = EF, triangle DEF is also an isosceles triangle.
We know that in triangle ABC:
- AB = BC implies that ∠A = ∠C (the angles opposite to the equal sides are equal).
- DE = EF implies that ∠D = ∠F (the angles opposite to the equal sides are equal).
Now we have:
- ∠B = ∠E (given)
- ∠A = ∠C (from triangle ABC)
- ∠D = ∠F (from triangle DEF)
We can now apply the SAS (Side-Angle-Side) congruence criterion:
- AB = EF (given)
- ∠B = ∠E (given)
- BC = DE (since BC = EF and DE = EF, we can say BC = DE)
- AB = EF
- ∠B = ∠E
- BC = DE
By the SAS criterion, triangle ABC is congruent to triangle DEF. Therefore, the correct statement is that both triangles are congruent and isosceles.
Topper's Solved these Questions
- IMO QUESTION PAPER 2017-18 SET-BBook:SCIENCE OLYMPIAD FOUNDATION Chapter:IMO QUESTION PAPER 2017-18 SET-BExercise:ACHIEVERS SECTION
Explore 5 Videos
- IMO QUESTION PAPER 2017-18 SET ABook:SCIENCE OLYMPIAD FOUNDATION Chapter:IMO QUESTION PAPER 2017-18 SET AExercise:ACHIEVERS SECTION
Explore 5 Videos
- IMO QUESTION PAPER 2018-19 SET -B Book:SCIENCE OLYMPIAD FOUNDATION Chapter:IMO QUESTION PAPER 2018-19 SET -B Exercise:ACHIEVERS SECTION
Explore 5 Videos
Similar Questions
Knowledge Check
In two triangle ABC and DEF, AB= DE ,BC=DF and AC =Ef then
A△ABC≅△DEFB△ABC≅△FEDC△ABC≅△ESEDNone of theseIn two triangles ABC and FDE, ∠B=∠D=90∘, AC = FE and BC = DE. Then ∠F = ____.
A∠CB∠AC∠BDcan't be determinedGiven two triangles ABC and DEF. If ΔABC~ΔDEF,2AB=DE and BC = 8 cm, then find the length of EF.
 A10cmB12cmC8cmD16cm
A10cmB12cmC8cmD16cm
In a triangle ABC, AB=BC and ∠A=60∘. Find ∠B.
View SolutionIn two congruent triangles ABC and DEF, if AB=DE and BC=EF. Name the pairs of equal angles.
View SolutionIf triangles ABC and DEF are similar such that 2AB = DE and BC = 8 cm, then what is EF equal to ?
View SolutionIf ΔABCandΔDEF are so related the ABFD=BCDE=CAEF, then which of the following is true?
View SolutionIn triangle ABC and DEF ,∠C=∠F,AC=DFandBC=EF . If AB = 2x - 1 and DE = 5x - 4 then the value of x is
View Solution