Inside an equiangular triangular park, there is a flower bed forming a similar triangle. Around the flower bed runs a uniform path of such a width that the sides of the park are exactly double the corresponding sides of the flower bed. The ratio of the areas of the path to the flower bed is
1:1
1:2
1:3
3:1
The correct Answer is:D
To solve the problem, we need to find the ratio of the areas of the path around the flower bed to the area of the flower bed itself. Let's break down the solution step by step.
Step 1: Understand the Problem
We have two similar triangles: one representing the equiangular triangular park (let's call it triangle ABC) and the other representing the flower bed inside it (let's call it triangle DEF). We know that the sides of triangle ABC are double the corresponding sides of triangle DEF.
Step 2: Assign Variables
Let the side length of triangle DEF (flower bed) be a. Therefore, the corresponding side length of triangle ABC (park) will be 2a.
Step 3: Use the Area Ratio Formula for Similar Triangles
For similar triangles, the ratio of their areas is equal to the square of the ratio of their corresponding side lengths. Thus, we can write:
Area of ABCArea of DEF=(Side of ABCSide of DEF)2
Substituting the side lengths:
Area of ABCArea of DEF=(2aa)2=(2)2=4
Step 4: Express Areas
Let:
- Area of triangle DEF = ADEF
- Area of triangle ABC = AABC
From the previous step, we have:
AABCADEF=4⟹AABC=4×ADEF
Step 5: Find the Area of the Path
The area of the path is the area of the park minus the area of the flower bed:
Area of Path=AABC−ADEF
Substituting AABC:
Area of Path=4ADEF−ADEF=3ADEF
Step 6: Find the Ratio of the Areas
Now, we can find the ratio of the area of the path to the area of the flower bed:
Area of PathADEF=3ADEFADEF=3
Thus, the ratio of the areas of the path to the flower bed is:
Ratio=3:1
Final Answer
The ratio of the areas of the path to the flower bed is 3:1.
---
We have two similar triangles: one representing the equiangular triangular park (let's call it triangle ABC) and the other representing the flower bed inside it (let's call it triangle DEF). We know that the sides of triangle ABC are double the corresponding sides of triangle DEF.
Let the side length of triangle DEF (flower bed) be a. Therefore, the corresponding side length of triangle ABC (park) will be 2a.
For similar triangles, the ratio of their areas is equal to the square of the ratio of their corresponding side lengths. Thus, we can write:
Let:
- Area of triangle DEF = ADEF
- Area of triangle ABC = AABC
The area of the path is the area of the park minus the area of the flower bed:
Now, we can find the ratio of the area of the path to the area of the flower bed:
The ratio of the areas of the path to the flower bed is 3:1.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERIMETER AND AREA EXERCISE - QUESTION BANK - 21(C)10videos
PERIMETER AND AREA
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERIMETER AND AREA EXERCISE - SELF ASSESSMENT SHEET10videos
PERIMETER AND AREA
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERIMETER AND AREA EXERCISE - QUESTION BANK - 21(A)19videos
PERIMETER AND AREA
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERCENTAGE AND ITS APPLICATIONSEXERCISE - Self Assessment Sheet - 1010videos
PERCENTAGE AND ITS APPLICATIONS
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALSEXERCISE - Self Assessment Sheet10videos
POLYGONS AND QUADRILATERALS
Similar Questions
Knowledge Check
- Question 1 - Select One
Twenty meters of wire is available for fencing a flower -bed in the form of a circular sector .Then the maximum area in square meters of the flower bed is
A12.5B10C25D30
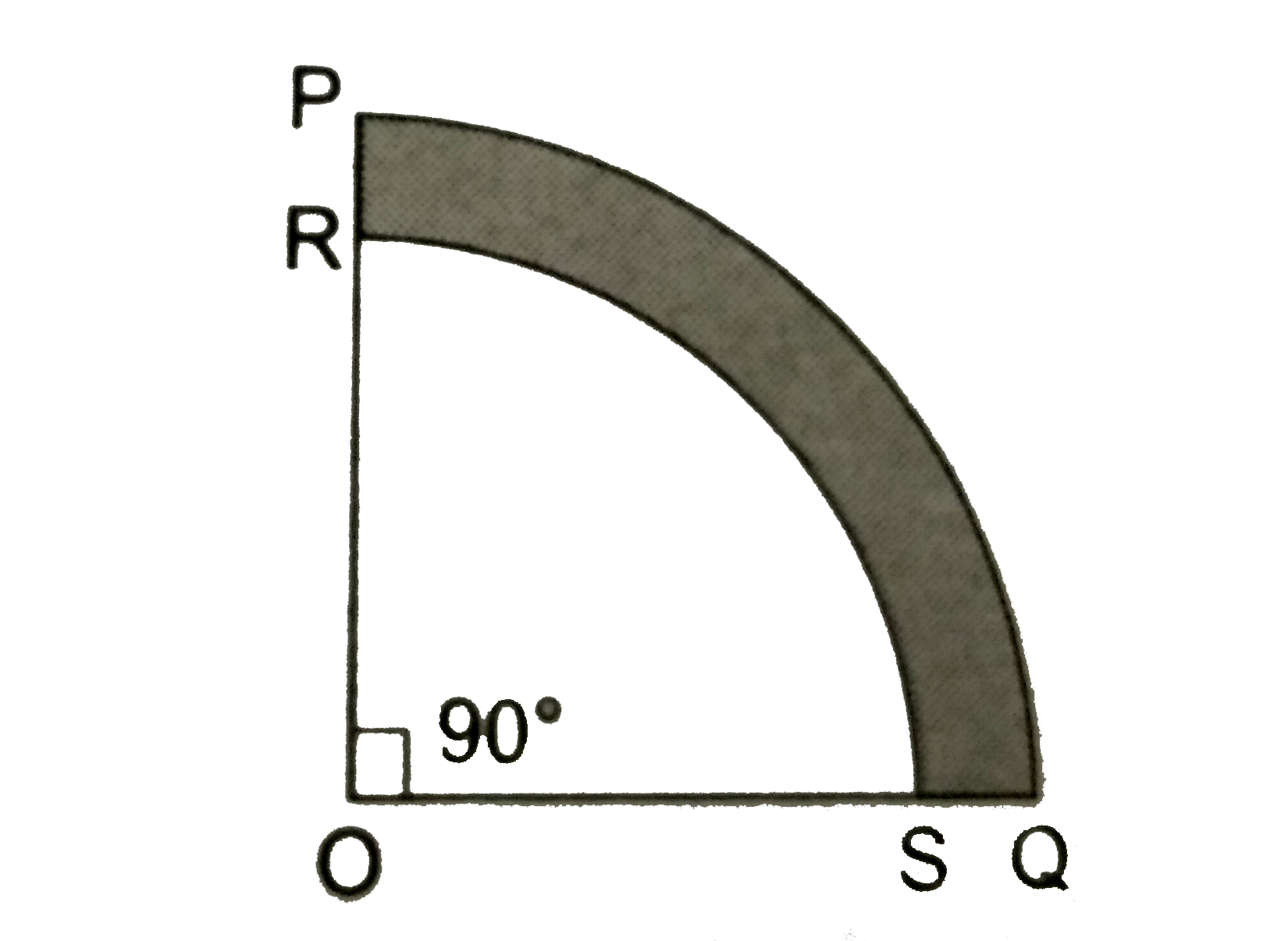
In the given figure, PQSR represents a flower bed. If OP=21m and OR=14m, find the area of the flower bed.
 View Solution
View SolutionThe perimeter of a square garden is 48m. A small flower bed covers 18sqm area inside this garden. What is the area of the garden that is not covered by the flower bed? What fractional part of the garden is covered by the flower bed and the remaining area?
View SolutionEach side of a square flower bed is 2 m 80 cm long. It is extended by digging a strip 30 cm wide all around it. Find the area of the enlarged flower bed and also the increase in the area of the flower bed.
View SolutionThere are two circular flower beds on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
View SolutionIn each of the corners, there is a flower bed in the form of a quadrant of a circle of radius 2 m. Also, there is a flower bed in the form of a circle of radius 2 m in the middle of the plot. Find the area of the remaining plot.
 View Solution
View SolutionA circular flower bed is surrounded by a path 4m wide. The diameter of the flower bed is 66m. What is the area of this path ? (π=3.14)
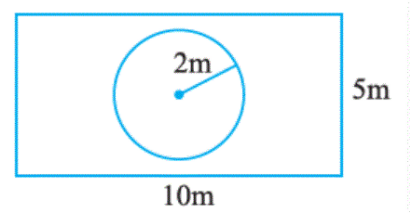
View SolutionThe adjoining figure represents a rectangular lawn with a circular flower bed in the middle. Find:
(i) the area of the whole land
(ii) the area of the flower bed
(iii) the area of the lawn excluding the area of the flower bed
(iv) the circumference of the flower bed.
 View Solution
View Solution


