It is given that ∠XYZ=64o and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP , find ∠XYQ and reflex∠QYP .
To solve the problem step by step, we will follow the instructions given in the question and use the properties of angles.
1. Draw the Figure:
- Start by drawing a line segment XY. Extend it to point P such that YP is a straight line.
- Mark point Z such that angle XYZ is formed at point Y with the given angle of 64°.
- Draw ray YQ such that it bisects the angle ZYP.
Hint: Remember that the angle XYZ is given as 64°, and YP is a straight line extending from XY.
2. Identify the Angles:
- We know that angle XYZ = 64°.
- Since XY is extended to P, angle ZYP is a linear pair with angle XYZ. Therefore, we can write:
∠XYZ+∠ZYP=180°
Hint: Use the property of linear pairs which states that two angles that form a straight line add up to 180°.
3. Calculate Angle ZYP:
- Substitute the known value into the equation:
64°+∠ZYP=180°
- Rearranging gives:
∠ZYP=180°−64°=116°
Hint: Always remember to subtract the known angle from 180° to find the other angle in a linear pair.
4. Use the Angle Bisector:
- Since ray YQ bisects angle ZYP, we have:
∠ZYQ=∠QYP=12∠ZYP
- Therefore:
∠ZYQ=∠QYP=12×116°=58°
Hint: The angle bisector divides the angle into two equal parts.
5. Find Angle XYQ:
- Now, we can find angle XYQ:
∠XYQ=∠XYZ+∠ZYQ
- Substitute the values:
∠XYQ=64°+58°=122°
Hint: To find the total angle at point Y, simply add the angles you have calculated.
6. Find Reflex Angle QYP:
- The reflex angle QYP can be calculated as:
Reflex ∠QYP=360°−∠QYP
- Since we know that:
∠QYP=58°
- Therefore:
Reflex ∠QYP=360°−58°=302°
Hint: The reflex angle is the larger angle formed by extending the angle beyond 180°.
Final Answers:
- ∠XYQ=122°
- Reflex ∠QYP=302°
- Start by drawing a line segment XY. Extend it to point P such that YP is a straight line.
- Mark point Z such that angle XYZ is formed at point Y with the given angle of 64°.
- Draw ray YQ such that it bisects the angle ZYP.
- We know that angle XYZ = 64°.
- Since XY is extended to P, angle ZYP is a linear pair with angle XYZ. Therefore, we can write:
∠XYZ+∠ZYP=180°
- Substitute the known value into the equation:
64°+∠ZYP=180°
- Rearranging gives:
∠ZYP=180°−64°=116°
- Since ray YQ bisects angle ZYP, we have:
∠ZYQ=∠QYP=12∠ZYP
- Therefore:
∠ZYQ=∠QYP=12×116°=58°
- Now, we can find angle XYQ:
∠XYQ=∠XYZ+∠ZYQ
- Substitute the values:
∠XYQ=64°+58°=122°
- The reflex angle QYP can be calculated as:
Reflex ∠QYP=360°−∠QYP
- Since we know that:
∠QYP=58°
- Therefore:
Reflex ∠QYP=360°−58°=302°
- ∠XYQ=122°
- Reflex ∠QYP=302°
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In Figure 1, y=√3xandz=2x. What is the ratio p:q:r in figure 2?
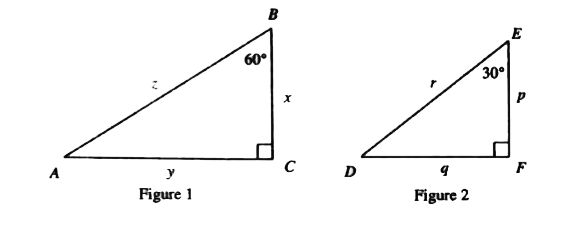 A1:2:3B√3:1:2C1:√3/2:1D2:√3:1
A1:2:3B√3:1:2C1:√3/2:1D2:√3:1
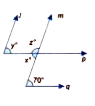
In the given figure l||mandp||q. Find the angle x,y, z
 View Solution
View SolutionIn the given figure, l||mandp||q. Find the angles x, y and z
 View Solution
View SolutionIn the figure, P is the centre of the circle. Prove that: ∠XPZ=2 (∠XZY+ ∠YXZ)
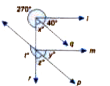
View SolutionIn the given figure, l||mandp||q. Find the angles x, y, z and t.
 View Solution
View SolutionIf p and q vary inversely, find the values of x,y and z.
 View Solution
View SolutionIf p and q vary inversely, find the values of x,y and z.
 View Solution
View SolutionGiven that P(3,1),Q(6.5), and R(x,y) are three points such that the angle PRQ is a right angle and the area of RQP is 7, find the number of such points R.
View Solution

