Question

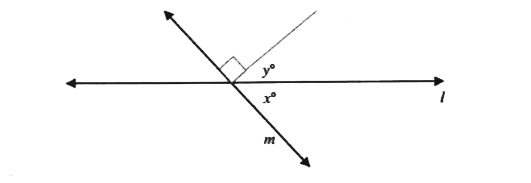
In figure, ${\displaystyle OA and OB}$
are opposite rays:

(i) If ${\displaystyle x={25}^0,}$
what is the value of ${\displaystyle y}$?

(ii) If ${\displaystyle y={35}^0,}$
what is the value of ${\displaystyle x}$?

Explanation

To solve the problem, we need to analyze the angles formed by the opposite rays OA and OB. Let's break it down step by step.

Step 1: Understand the relationship of angles
Since OA and OB are opposite rays, the angle AOB forms a straight line. Therefore, the measure of angle AOB is 180 degrees.

Step 2: Set up the equation
From the problem, we know:
- Angle AOC = 2y + 5 degrees
- Angle COB = 3x degrees

Since angle AOB is the sum of angles AOC and COB, we can write the equation:
\( \text{Angle AOB} = \text{Angle AOC} + \text{Angle COB} \)
This gives us:
\( 180 = (2y + 5) + (3x) \)
Rearranging this, we get:
\( 2y + 3x + 5 = 180 \)
Subtracting 5 from both sides:
\( 2y + 3x = 175 \)
Let’s call this Equation 1.

Step 3: Solve for (i) when \( x = 25^\circ \)
Substituting \( x = 25^\circ \) into Equation 1:
\( 2y + 3(25) = 175 \)
This simplifies to:
\( 2y + 75 = 175 \)
Subtracting 75 from both sides:
\( 2y = 175 - 75 \)
\( 2y = 100 \)
Dividing both sides by 2:
\( y = 50^\circ \)

Step 4: Solve for (ii) when \( y = 35^\circ \)
Now substituting \( y = 35^\circ \) into Equation 1:
\( 2(35) + 3x = 175 \)
This simplifies to:
\( 70 + 3x = 175 \)
Subtracting 70 from both sides:
\( 3x = 175 - 70 \)
\( 3x = 105 \)
Dividing both sides by 3:
\( x = 35^\circ \)

Final Answers
(i) If \( x = 25^\circ \), then \( y = 50^\circ \).

(ii) If \( y = 35^\circ \), then \( x = 35^\circ \).