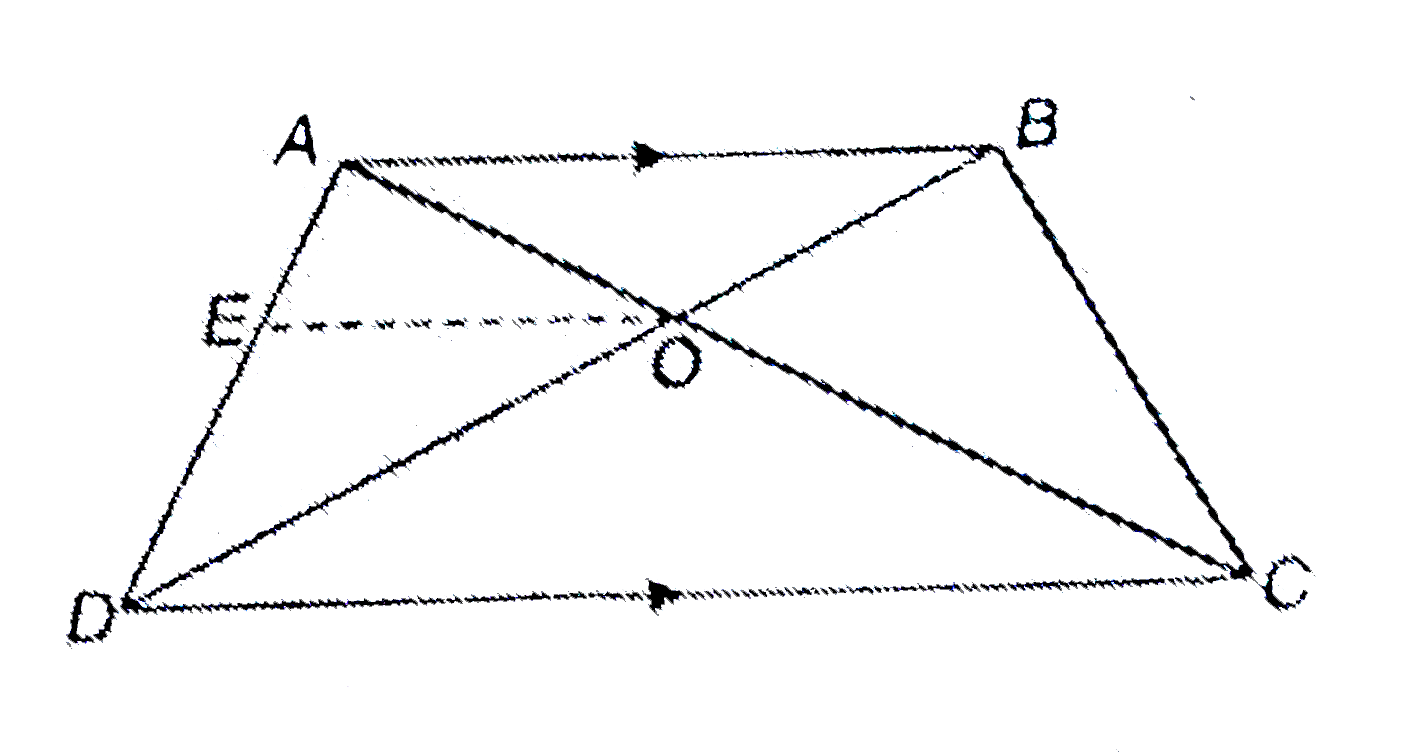
Kamala have drawn a trapezium $P Q R S$ of which $P Q ∣ ∣ S R$ . If the diagonals $P R$ and $Q S$ intersect each other at $O$ , then prove that $O P : O R = O Q : O S$ , If $S R = 2 P Q$ , then prove that $O$ is a point of trisection of both the diagonals.

Video Solution

|

Answer

Step by step video & image solution for Kamala have drawn a trapezium PQRS of which PQ||SR. If the diagonals PR and QS intersect each other at O, then prove that OP:OR=OQ:OS, If SR=2PQ, then prove that O is a point of trisection of both the diagonals. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
A $1 : 4$
B $1 : 2$
C $4 : 1$
D $2 : 1$
Question 2 - Select One
ABCD is a trapezium in which $A B ∣ ∣ C D$ and $A B = 2 C D$ . It its diagonals intersect each other at O then ratio of the area of triangle AOB and COD is
A $1 : 2$
B $2 : 1$
C $1 : 4$
D $4 : 1$

UNIQUE PUBLICATION-SIMILARITY-Assignment-I

Home
Ask Doubt
Profile