PQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ
In cyclic quadrilateral
PQRS:
PQ∣∣RS
⇒PR=QS
We know from the properties of circle,
OP⋅OR=Hoq⋅OS
Above can also be written as
OP⋅(OP+PR)=OQ⋅(OQ+QS)
⇒OP2−OQ2=QS(OQ−OP)
⇒(OP−OQ)(OP+OQ+QS)=0
∴OP=OQ
Hence proved.
Topper's Solved these Questions
Similar Questions
PQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If PQ=16 cm and RS=12 cm, find the distance between PQ and RS, if they lie: on opposite side of the centre O
View SolutionPQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If PQ=16 cm and RS=12 cm, find the distance between PQ and RS, if they lie: on the same side of centre O
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q as shown in figure. Show that ABC≅CDA.
 View Solution
View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
View SolutionIn Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that: PL=QM (ii) LO=OM
View SolutionPQRS is a parallelogram. PXandQY are respectively, the perpendiculars from PandQ to SRandRS produced. Prove that PX=QY
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
 View Solution
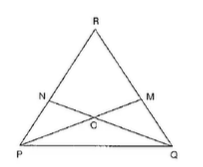
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
 View Solution
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View Solution

