Let a, b, c be the side-lengths of a triangle, and l, m,n be the lengths of its medians. Put K=(l+m+na+b+c) Then, as a, b, c vary, K can assume every value in the interval

A

(14,45)

B

(12,45)

C

(34,1)

D

(45,54)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

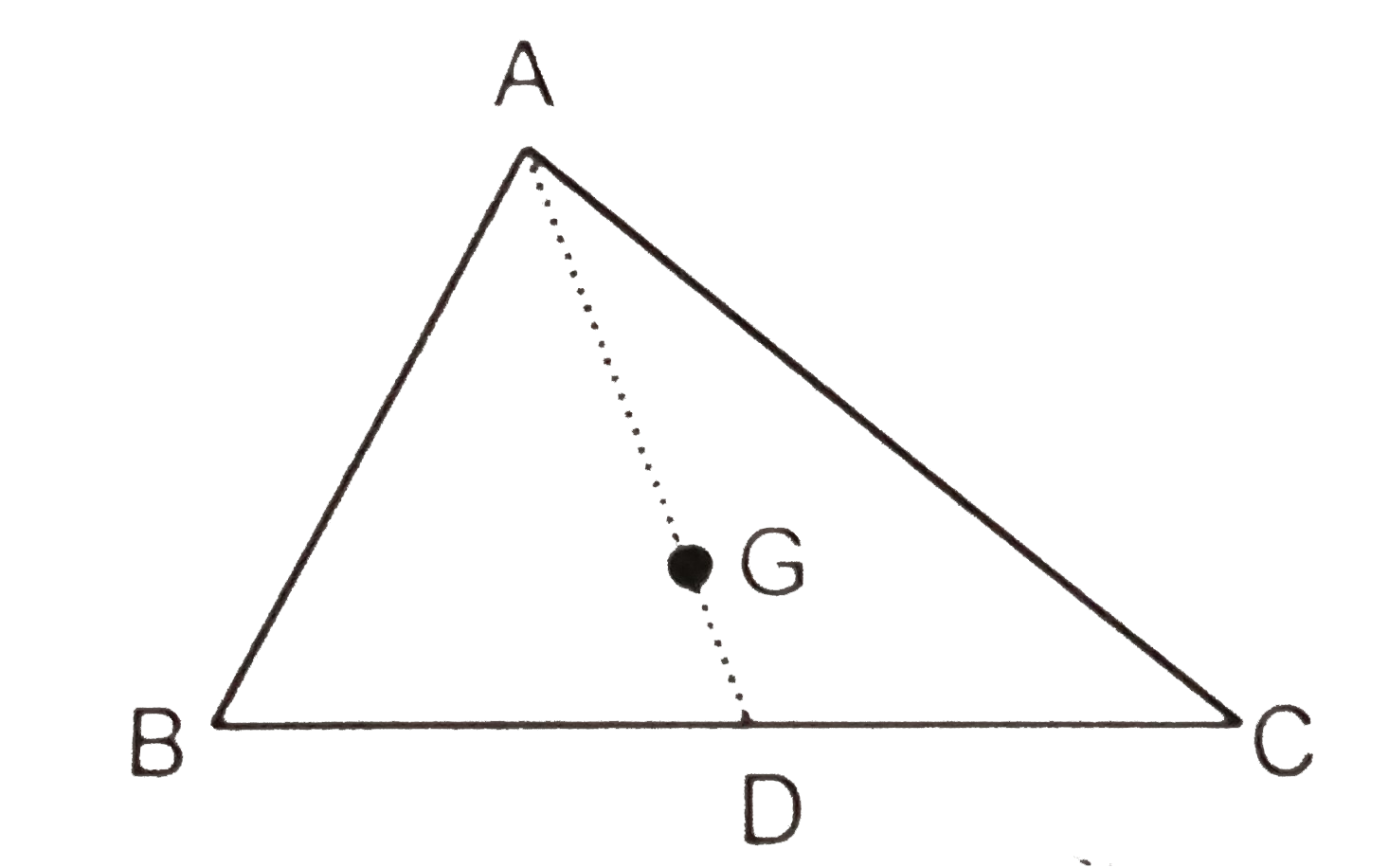
ocr_image
As Ad is medium ⇒AD<AB+AC2
⇒l<b+c2
Similarly m<c+a2 and n<a+b2
⇒l+m+n<a+b+c
⇒l+m+n<a+b+c
⇒l+m+na+b+c<1 (i)
Also in the ΔBGC
BG+GC>BC
⇒23(m+n)>a
Similarly 23(n+l)>b
and 23(l+m)>c
Hence 43(l+m+n)>a+b+c
l+m+na+b+c>34 (ii)
By (i) and (ii) l+m+na+b+c∈(34,1)

Updated on:21/07/2023
|
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If a, b,c are the lengths of the sides of triangle , then

    Aa−b>c
    Ba+b<c
    Cc=a+b
    Dc<a+b

  • Let a,b,c be the sides of a triangle ABC, a=2c,cos(A-C)+cos B=1. then the value of C is

    Aπ/6
    Bπ/3
    C2π/3
    D5π/6

  • Let a = BC, b = CA, c = AB be side lengths of a triangle ABC. And m be the length of the median through A. If a = 8, b-c = 2, m = 6, then the nearest integer to b is

    A7
    B8
    C9
    D10