Let a function f(x) be defined in [−2,2] as
f(x)=⎧⎪⎨⎪⎩{x},−2≤x<−1|sgn x|,−1≤x≤1{−x},1<x≤2 where {x} and sgn x denote fractional part and signum functions, respectively. Then find the area bounded by the graph of f(x) an the x-axis.
Video Solution
Text Solution
f(x)=⎧⎪⎨⎪⎩{x},−2≤x<−1|sgn x|,−1≤x≤1{−x},1<x≤2
=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
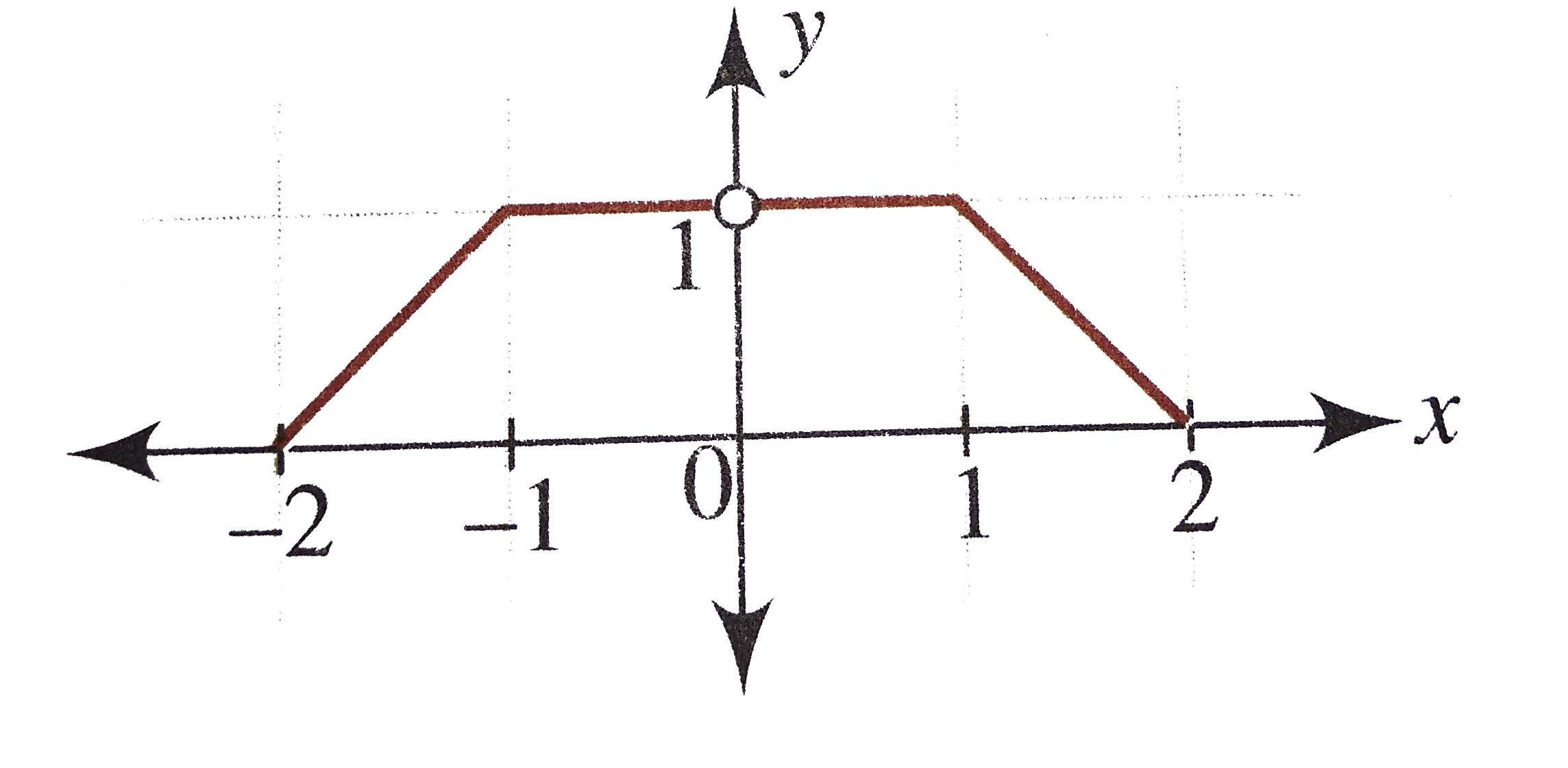
⎪⎩x+2,−2≤x<−11,−1≤x<0,0,x=01,0<x≤1−x+2,1<x≤2
The graph fo the function is as shown in the following figure.
Area =2+42×1=3 sq. units
|
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Knowledge Check
Let function f(x) is defined in [−2,2] as f(x)=⎧⎪⎨⎪⎩{x},−2≤x≤−1|sgnx|,−1≤x≤1{−x},1<x≤2 where {x} and sgn x denotes fractional part and signum functions, respectively. Then the area bounded by the graph of f(x) and x-axis is
A2 sq. unitsB3 sq. unitsC4 sq. unitsD5 sq. unitsConsider a function defined in [−2,2]
f(x)=⎧⎪⎨⎪⎩{x}−2l≤x<−1|sgnx|−1≤x≤1{−x}1<x≤2, where {.} denotes the fractional part function.
The total number of points of discontinuity of f(x) for x∈[−2,2] is:A0B1C2D4Consider a function defined in [−2,2]
f(x)=⎧⎪⎨⎪⎩{x}−2≤x<−1|sgnx|−1≤x≤1{−x}1<x≤2, where {.} denotes the fractional part function.
The number of points for x∈[−2,2] where f(x) is non-differentiable is:A0B1C2D3
If a function f(x) is defined as f(x)=⎧⎪⎨⎪⎩−x,x<0x2,0≤x≤1x2−x+1,x>1 then
View SolutionLet f(x) be defined on [-2,2] and is given by
f(x) = {x+1−2≤x≤0x−10≤x≤2, then f (|x|) is defined as
View SolutionIf f(x)=⎧⎪⎨⎪⎩x, for 0≤x<12, for x=1x+1, for 1<x≤2, then f is
View SolutionIf f(x)={3x2+12x−1,−1≤x≤237−x,2<x≤3,then
View SolutionConsider the function f(x)=[x{x}+1,if0≤x<12−{x},if1≤x≤2, where {x} denotes the fractional part function. Which one of the following statements is not correct ?
View Solution
