Question

Let $a\in R$
and let $f:R\overrightarrow{}$
be given by $f\left(x\right)=x^5-5x+a,$
then


(a) $f\left(x\right)$
has three real roots if $a>4$

(b)$f\left(x\right)$
has only one real roots if $a>4$

(c)$f\left(x\right)$
has three real roots if $a<-4$

(d)$f\left(x\right)$
has three real roots if $-4<a<4$

Explanation

Let `=f(x)=x^(5)-5x`
`rArr f'(x)=5x^(4)-5`
`=5(x^(4)-1)`
`=5(x-1)(x+1)(x^(2)+1)`
`f'(x)=0, :. x=-1, 1`
`f''(x)=20x^(3)`
`f''(1)=20` and `f''(-1)=-20`
So x = 1 is the point of minima and x = -1 is the point of maxima.
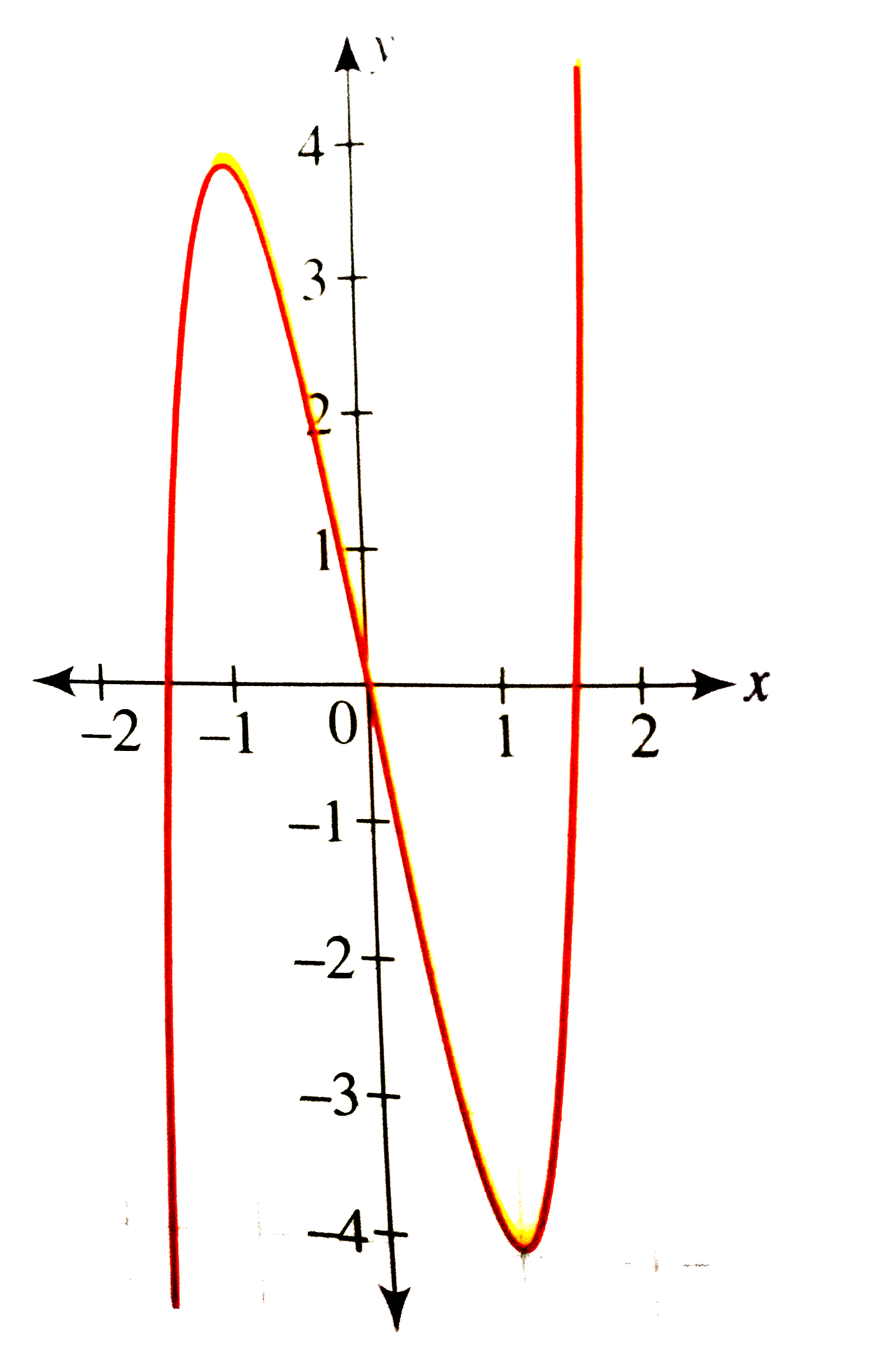
Also `f(1)=-4` and `f(-1)=4`
Graph of `y=f(x)` is as shown in the adjacent figure.
From the graph, `x^(5)-5x=-a` has one real root if `-a lt -4` or `-agt4`,
i.e. `a gt 4 ` or `a lt -4`
Also `x^(5)-5x=-a` has three real roots if `-4lt -a lt 4`
i.e. `-4 lt a lt 4`
Hence correct answers are (b) and (d).