Let A(a,0)andB(b,0) be fixed distinct points on the x-axis, none of which coincides with the O(0,0), and let C be a point on the y-axis. Let L be a line through the O(0,0) and perpendicular to the line AC. The locus of the point of intersection of the lines L and BC if C varies along is (provided c2+ab≠0)Solution in Bengali
(a) x2a+y2b=x
(b) x2a+y2b=y
(c) x2b+y2a=x
(d) x2b+y2a=y
The correct Answer is:C
Equation of the line L is y=acx
As (h,k) lies on it, hence
k=ach (i)
Now equation of BC
xb+yc=1
(h,k) lies on it
∴hb+kc=1
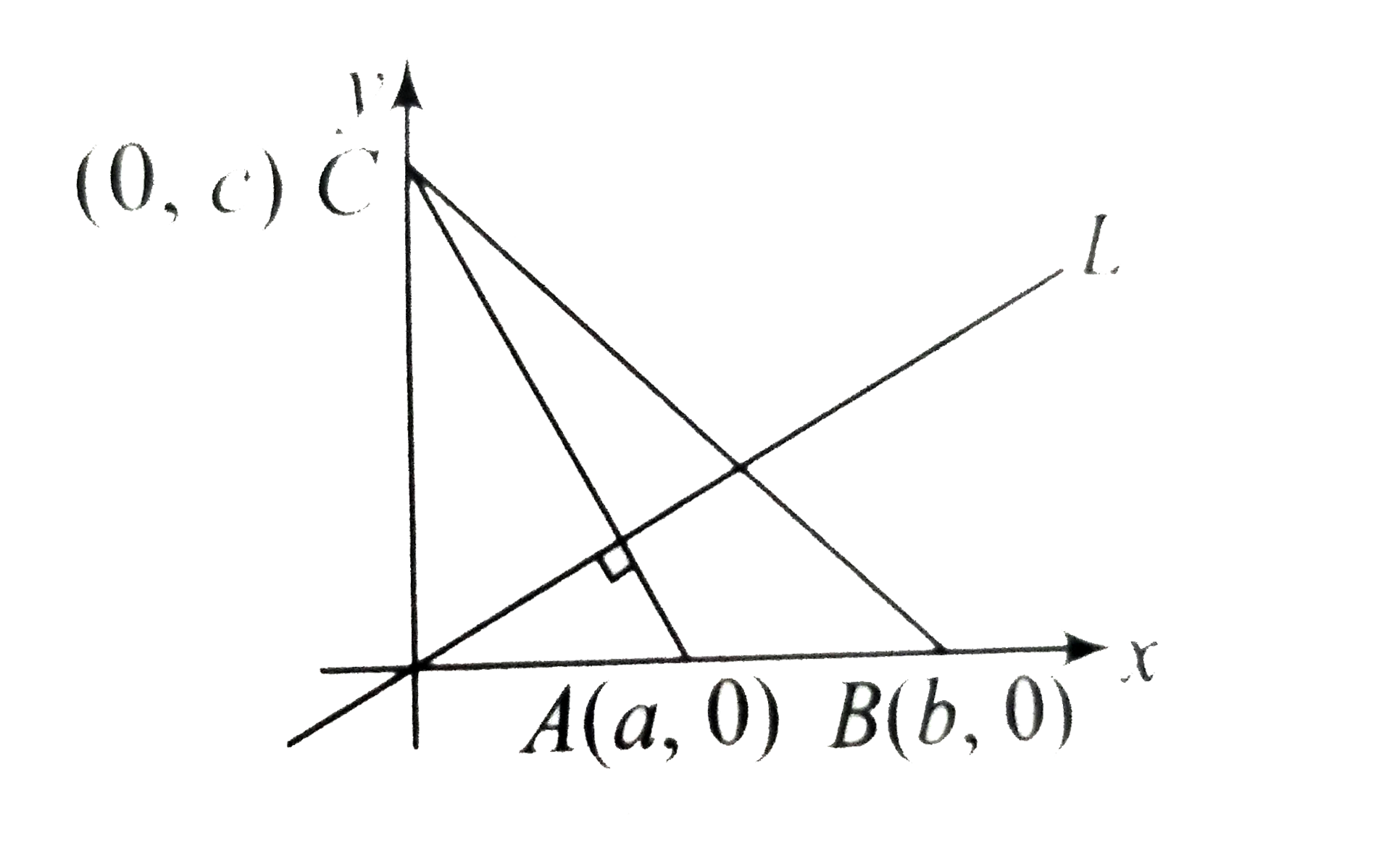
Substituting c=ahk in (ii) from (i)
h2hb+k2ah=1
∴ Locus of P is x2b+y2a=x
Topper's Solved these Questions
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- STATISTICSBOOK - CENGAGE PUBLICATIONCHAPTER - STATISTICSEXERCISE - Archives
10 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
Similar Questions
The point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionIf the mean deviation of the numbers 1,1+d,1+2d,...,1+100d from their mean is 255, then the d is equal to
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionLet A(a,0) and B(b,0) be fixed distinct points on the x-axis, none of which coincides with the O(0,0), and let C be a point on the y-axis. Let L be a line through the O(0,0) and perpendicular to the line AC. The locus of the point of intersection of the lines L and BC if C varies along is (provided c^2 +ab != 0)
View Solution91. Let A(a, 0) and B(b, 0) be fixed distinct points on the r-axis, none of which coincides with the origin O(0, 0) and let Cbe a point on the y-axis. Let L be a line through the O(0, 0) and perpendicular to the line AC. The locus of the point of intersection of the lines L and BC if C varies along the y-axis, is (provided c2 + a04 0) (6) 2 and loc
View SolutionIf the parabola y=(a-b)x^(2)+(b-c)x+(c-a) touches x -axis then the line ax+by+c=0 passes through a fixed point
View SolutionFind the point which equisdistant from points O(0,0,0),A(a,0,0)B(0,b,0)andC(0,0,c)
View SolutionThe point equidistant from the O(0,0,0),A(a,0,0),B(0,b,0) and C(0,0,c) has the coordinates
View SolutionA(−3,3) B(0,0) C(3,−3) బిందువులు సరేఖియాలని భూపుము.
View SolutionIf a,b,c are in harmonic progression, then the straight line ((xa))+(yb)+(lc)=0 always passes through a fixed point. Find that point.
View SolutionLet A(a,0)andB(b,0) be fixed distinct points on the x-axis, none of which coincides with the O(0,0), and let C be a point on the y-axis. Let L be a line through the O(0,0) and perpendicular to the line AC. The locus of the point of intersection of the lines L and BC if C varies along is (provided c2+ab≠0)
View SolutionLet O (0,0) and A (0, 1) be two fixed points, then points P for which DeltaAOP The perimeter is 4, the point is
View SolutionFour points O(0,0,0),A(l,0,0),B(0,m,0) And C(0,0,n) Find the coordinates of a point equidistant from
View SolutionLet A be any point on the x-axis and B=(2,3). The perpendicular at A to the line AB meets the y-axis at C. Then the locus of midpoint of segment AC as A moves is given by
View Solution
