Let AP and BQ be two vertical poles at points A and B respectively. If AP = 16 m, BQ = 22m and AB = 20 m, then find the distance of a point R on AB from the point A such that RP2+RQ2 is minimum.Solution in Gujrati
The correct Answer is:10 meter
Step by step video, text & image solution for Let AP and BQ be two vertical poles at points A and B respectively. If AP = 16 m, BQ = 22m and AB = 20 m, then find the distance of a point R on AB from the point A such that RP^(2)+RQ^(2) is minimum. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATION OF DERIVATIVES BOOK - KUMAR PRAKASHANCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - SOLUTIONS OF NCERT EXEMPLAR PROBLEMS (SHORT ANSWER TYPE QUESTIONS)
24 Videos
- APPLICATION OF DERIVATIVES BOOK - KUMAR PRAKASHANCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - SOLUTIONS OF NCERT EXEMPLAR PROBLEMS (LONG ANSWER TYPE QUESTIONS)
10 Videos
- APPLICATION OF DERIVATIVES BOOK - KUMAR PRAKASHANCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - TEXTBOOK BASED MCQS
83 Videos
- ANNUAL EXAMINATION :SAMPLE PAPERBOOK - KUMAR PRAKASHANCHAPTER - ANNUAL EXAMINATION :SAMPLE PAPEREXERCISE - PART-B ( SECTION-C)
10 Videos
- APPLICATION OF INTEGRALSBOOK - KUMAR PRAKASHANCHAPTER - APPLICATION OF INTEGRALSEXERCISE - PRACTICE PAPER ( SECTION -D)
2 Videos
Similar Questions
A spherical ball of salt is dissolving in water in such a manner that the rate of decrease of the volume at any instant is propotional to the surface. Prove that the radius is decreasing at a constant rate.
Hint for solution : Take volume V and curve surface are S of spherical ball. Calculate by taking dVdtαS.
View SolutionIf the sum of the lengths of the hypotenuse and a side of a right angled triangle is given, show that the area of the triangle is maximum when the angle between them is π3.
View SolutionIf x and y are the sides of two squares such that y=x−x2. Then the rate of change, if the area of second square with respect to the first square, when x = 2, is ……….
View Solutionshow that
⎡⎢ ⎢⎣(x+y)2zxzyzx(z+y)2xyzyxy(z+x)2⎤⎥ ⎥⎦=2xyz(x+y+z)3
View SolutionFind the area of the regaion enclosed by {(x,y):y2≤4x,4x2+4y2≤9}.
View SolutionLet AP and BQ be two vertical poles at points A and B, respectively. If AP=16m,BQ=22mandAB=20m, then find the distance of a point R on AB from the point A such that RP2+RQ2is minimum.
View SolutionIn Figure, AP and BQ are perpendiculars to the line segment AB and AP=BQ. Prove that O is the mid-point of line segment AB and PQ.
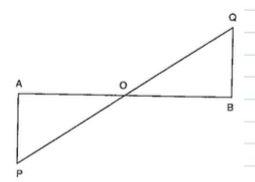
View SolutionIn Figure, AP and BQ are perpendiculars to the line segment AB and AP=BQ . Prove that O is the mid-point of line segment AB and PQ
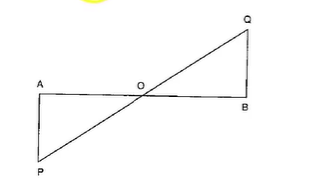
View SolutionLet AP and BQ be two vertical poles at points A and B respectively. If AP=16m, BQ=22m and AB=20m , then find the distance of a point R on AB from the point A such that RP2+RQ2 is minimum.
View Solutionमान लीजिए बिंदु A और B पर क्रमशः AP तथा BQ दो उर्ध्वाधर स्तंभ है| यदि AP = 16 m, BQ = 22 m और AB = 20 m हों तो AB पर एक ऐसा बिंदु R ज्ञात कीजिए ताकि RP2+RQ2 निम्नतम है |
View Solutionमान लीजिए बिंदु A और B पर क्रमशः AP तथा BQ दो ऊध्वर्रधकर स्तम्भ है । यदि AP =16 मि, BQ =22 मि और AB = 20 मि हो तो AB पर एक ऐसा बिंदु R ज्ञात कीजिए ताकि RP2+RQ2 निम्नतम हो।
View SolutionThe line segments AB and PQ intersect each other at the point C. AP and BQ are perpendiculars on AB respectively. If CA=20cm, CB=8cm and AP=10cm, then find the value of BQ.
View SolutionIf the tangent at the point (a,b) on the curve x3+y3=a3+b3 meets the curve again at the point (p,q) then
1) ab+pq=0 2) bq+ab+ap=0 3) bp+aq+ab=0 4) bq+pq+ap=0
View SolutionLet AP and BQ be two vertical poles at points A and B, respectively. If AP = 16 m, BQ = 22 m and AB = 20 m, then find the distance of a point R on AB from the point A such that RP2+RQ2 is minimum.
View SolutionLet AP and BQ be two vertical poles at points A and B, respectively. If AP = 16 m, BQ = 22 m and AB = 20 m, then find the distance of a point R on AB from the point A such that RP2+RQ2 is minimum.
View Solution
