Let C1and C2 be two circles with C2 lying inside C1 A circle C lying inside C1 touches C1 internally and C2 externally. Identify the locus of the centre of CSolution in Punjabi
The correct Answer is:∴ Locus of O is an ellipse with foci O1andO2.
Step by step video & image solution for Let C_1and C_2 be two circles with C_2 lying inside C_1 A circle C lying inside C_1 touches C_1 internally and C_2 externally. Identify the locus of the centre of C by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLE BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - EXAMPLE
2 Videos
- CIRCLE BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise For Session 1
18 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
3 Videos
Similar Questions
Evaluate the given limit : limx→0(x+1)5−1x+1
View SolutionEvaluate the given limit limx→0(cosecx−cotx)
View SolutionThe value of (300)(3010)−(301)(3011)+(302)(3012)+....+(3020)(3030)
View SolutionFind the modules of 2+3ι
View SolutionThe centres of two circles C_1 and C_2, each of unit radius are at a distance of 6 units from each other. Let P be the mid point of the line segment joining the centres of C_1 and C_2, and C be a circle touching circles C_1 and C_2 externally. If a common tangent to C_1 and C passing through P is also a common tangent to C_2 and C. then the radius of the circle C is.
View SolutionLet C,C_1,C_2 be circles of radii 5,3,2 respectively. C_1 and C_2, touch each other externally and C internally. A circle C_3 touches C_1 and C_2 externally and C internally. If its radius is m/n where m and n are relatively prime positive integers, then 2n-m is:
View SolutionC_1 and C_2 are fixed circles of radii r_1 and r_2 touches each other externally. Circle 'C' touches both Circles C_1 and C_2 extemelly. If r_1/r_2=3/2 then the eccentricity of the locus of centre of circles C is
View SolutionA,B,C are the centres of the three circles C1,C2,C3 such that C1,C2 touch each other exernally and they both touch C3 from inside then the radical centre of the circles is for triangle ABC is
View SolutionLet C1and C2 be two circles with C2 lying inside C1 A circle C lying inside C1 touches C1 internally and C2 externally. Identify the locus of the centre of C
View SolutionConsider three circles C1,C2andC3 such that C2 is the director circle of C1,andC3 is the director circle of C2. Tangents to C1, from any point on C3 intersect C2, at PandQ. Find the angle between the tangents to C2 at P and Q. Also identify the locus of the point of intersec- tion of tangents at PandQ.
View SolutionLet C,C1,C2 be circles of radii 5,3,2 respectively. C1 and C2, touch each other externally and C internally. A circle C3 touches C1 and C2 externally and C internally. If its radius is mn where m and n are relatively prime positive integers, then 2n-m is:
View Solutionदिखाए गये चित्रानुसार दोनो वृतों के केंद्रों C1 तथा C2 के मध्य दुरी 35 है अर्थात C1C2=35 तथा C1 व C2 केंद्रों वाले वृतों की त्रिज्याएँ क्रमशः 12 व 9 है । यदि वृतों की उभयनिष्ठ आंतरिक स्पर्श रेखा तथा C1C2 का प्रतिच्छेद बिंदु P है, तो l(C1P) का मान होगा
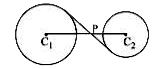
(i) 18 (ii) 20 (iii) 12 (iv) 15
View SolutionThe centres of two C1 and C2, each unit of unit radii, are at a distance of 6 units from each other. Let P be the mid-point of the line segment joining the centres of C1andC2. A third circle C is drawn such that it is externally tangent to both the circles C1andC2 at the same points where the lines passing through P are tangent to the circles C1andC2. The radius of the circle C is
View SolutionIn the figure given, two circles with centres Ct and C2 are 35 units apart, i.e. C1C2=35. The radii of the circles with centres C1 and C2 are 12 and 9 respectively. If P is the intersection of C1C2 and a common internal tangent to the circles, then l(C1P) equals
View SolutionC1andC2 are fixed circles of radii r1andr2 touches each other externally. Circle 'C' touches both Circles C1andC2 extemelly. If r1r2=32 then the eccentricity of the locus of centre of circles C is
View Solution
