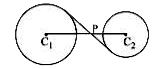
In the figure given, two circles with centres Ct and C2 are 35 units apart, i.e. C1C2=35. The radii of the circles with centres C1 and C2 are 12 and 9 respectively. If P is the intersection of C1C2 and a common internal tangent to the circles, then l(C1P) equalsSolution in Tamil
The correct Answer is:20
Step by step video & image solution for In the figure given, two circles with centres C_t and C_2 are 35 units apart, i.e. C_1 C_2=35. The radii of the circles with centres C_1 and C_2 are 12 and 9 respectively. If P is the intersection of C_1 C_2 and a common internal tangent to the circles, then l(C_1 P) equals by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the diagram as shown, a circle is drawn with centre C(1, 1) and radius I and a line L. The line Lis tangential to the circle at Q. Further L meet the y-axis at R and the x-axis at Pis such a way that the angle OPQ equals θ where 0<θ<π2 The coordinates of Q are
View SolutionFind the derivative of y=ln(cosx2).
View SolutionLet z=x+iy be a complex number where xandy are integers. Then, the area of the rectangle whose vertices are the roots of the equation zz3+zz3=350 is 48 (b) 32 (c) 40 (d) 80
View SolutionThe centres of two circles C_1 and C_2, each of unit radius are at a distance of 6 units from each other. Let P be the mid point of the line segment joining the centres of C_1 and C_2, and C be a circle touching circles C_1 and C_2 externally. If a common tangent to C_1 and C passing through P is also a common tangent to C_2 and C. then the radius of the circle C is.
View SolutionC_1 and C_2 are fixed circles of radii r_1 and r_2 touches each other externally. Circle 'C' touches both Circles C_1 and C_2 extemelly. If r_1/r_2=3/2 then the eccentricity of the locus of centre of circles C is
View SolutionLet C1and C2 be two circles with C2 lying inside C1 A circle C lying inside C1 touches C1 internally and C2 externally. Identify the locus of the centre of C
View SolutionTwo circles C1 and C2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB and QY meets circles C1 andC2 at Xa n dZ respectively. Then prove that Y is the midpoint of XZ
View SolutionConsider three circles C1,C2andC3 such that C2 is the director circle of C1,andC3 is the director circle of C2. Tangents to C1, from any point on C3 intersect C2, at PandQ. Find the angle between the tangents to C2 at P and Q. Also identify the locus of the point of intersec- tion of tangents at PandQ.
View SolutionTransverse common tangents are drawn from O to the two circles C1,C2 with 4, 2 respectively. Then the ratio of the areas of triangles formed by the tangents drawn from O to the circles C1andC2 and chord of contacts of O w.r.t the circles C1andC2 respectively is
View Solutionदिखाए गये चित्रानुसार दोनो वृतों के केंद्रों C1 तथा C2 के मध्य दुरी 35 है अर्थात C1C2=35 तथा C1 व C2 केंद्रों वाले वृतों की त्रिज्याएँ क्रमशः 12 व 9 है । यदि वृतों की उभयनिष्ठ आंतरिक स्पर्श रेखा तथा C1C2 का प्रतिच्छेद बिंदु P है, तो l(C1P) का मान होगा
(i) 18 (ii) 20 (iii) 12 (iv) 15
View SolutionThe centres of two C1 and C2, each unit of unit radii, are at a distance of 6 units from each other. Let P be the mid-point of the line segment joining the centres of C1andC2. A third circle C is drawn such that it is externally tangent to both the circles C1andC2 at the same points where the lines passing through P are tangent to the circles C1andC2. The radius of the circle C is
View SolutionIn the figure given, two circles with centres Ct and C2 are 35 units apart, i.e. C1C2=35. The radii of the circles with centres C1 and C2 are 12 and 9 respectively. If P is the intersection of C1C2 and a common internal tangent to the circles, then l(C1P) equals
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 and C1 Q are in
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
View SolutionLet C1and C2 be two circles with C2 lying inside C1 circle C lying inside C1 touches C1 internally andexternally. Identify the locus of the centre of C
View Solution
