Let Δ denote the area of the ΔABCandΔp be the area of its pedal triangle. If Δ=kΔp, then k is equal to
The correct Answer is:12cosAcosBcosC
To solve the problem, we need to find the value of k such that the area of triangle ABC (denoted as Δ) is equal to k times the area of its pedal triangle Δp.
1. Understanding the Pedal Triangle:
The pedal triangle DEF is formed by dropping perpendiculars from the vertices A,B,C of triangle ABC onto the opposite sides. The vertices of the pedal triangle are the feet of these perpendiculars.
2. Area of the Pedal Triangle:
The area Δp of the pedal triangle can be expressed using the lengths of its sides and the sine of the angles between them. The sides of the pedal triangle can be expressed in terms of the sides of triangle ABC and the angles at its vertices:
- DE=CcosC
- EF=AcosA
- FD=BcosB
Therefore, the area Δp can be calculated as:
Δp=12×DE×EF×sinD
Substituting the expressions for DE and EF:
Δp=12×(CcosC)×(BcosB)×sin(180∘−2A)
Since sin(180∘−x)=sinx, we have:
Δp=12×C×B×cosC×cosB×sin(2A)
Using the identity sin(2A)=2sinAcosA, we can rewrite it as:
Δp=12×C×B×cosC×cosB×2sinAcosA
Simplifying gives:
Δp=C×B×cosC×cosB×sinAcosA
3. Area of Triangle ABC:
The area Δ of triangle ABC can be expressed as:
Δ=12×B×C×sinA
4. Relating the Two Areas:
We know from the problem statement that:
Δ=kΔp
Substituting the expressions for Δ and Δp:
12×B×C×sinA=k×(C×B×cosC×cosB×sinAcosA)
5. Solving for k:
Dividing both sides by C×B×sinA (assuming sinA≠0):
12=k×cosC×cosB×cosA
Rearranging gives:
k=12cosAcosBcosC
Final Result:
Thus, the value of k is:
k=12cosAcosBcosC
The pedal triangle DEF is formed by dropping perpendiculars from the vertices A,B,C of triangle ABC onto the opposite sides. The vertices of the pedal triangle are the feet of these perpendiculars.
The area Δp of the pedal triangle can be expressed using the lengths of its sides and the sine of the angles between them. The sides of the pedal triangle can be expressed in terms of the sides of triangle ABC and the angles at its vertices:
- DE=CcosC
- EF=AcosA
- FD=BcosB
Δp=12×DE×EF×sinD
Substituting the expressions for DE and EF:
Δp=12×(CcosC)×(BcosB)×sin(180∘−2A)
Since sin(180∘−x)=sinx, we have:
Δp=12×C×B×cosC×cosB×sin(2A)
Using the identity sin(2A)=2sinAcosA, we can rewrite it as:
Δp=12×C×B×cosC×cosB×2sinAcosA
Simplifying gives:
Δp=C×B×cosC×cosB×sinAcosA
The area Δ of triangle ABC can be expressed as:
Δ=12×B×C×sinA
We know from the problem statement that:
Δ=kΔp
Substituting the expressions for Δ and Δp:
12×B×C×sinA=k×(C×B×cosC×cosB×sinAcosA)
Dividing both sides by C×B×sinA (assuming sinA≠0):
12=k×cosC×cosB×cosA
Rearranging gives:
k=12cosAcosBcosC
Thus, the value of k is:
k=12cosAcosBcosC
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Knowledge Check
What is the area of the triangle?
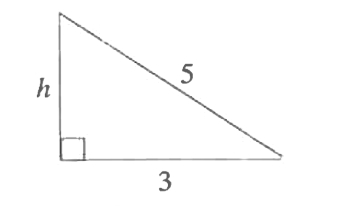 A6B7.5C8D11
A6B7.5C8D11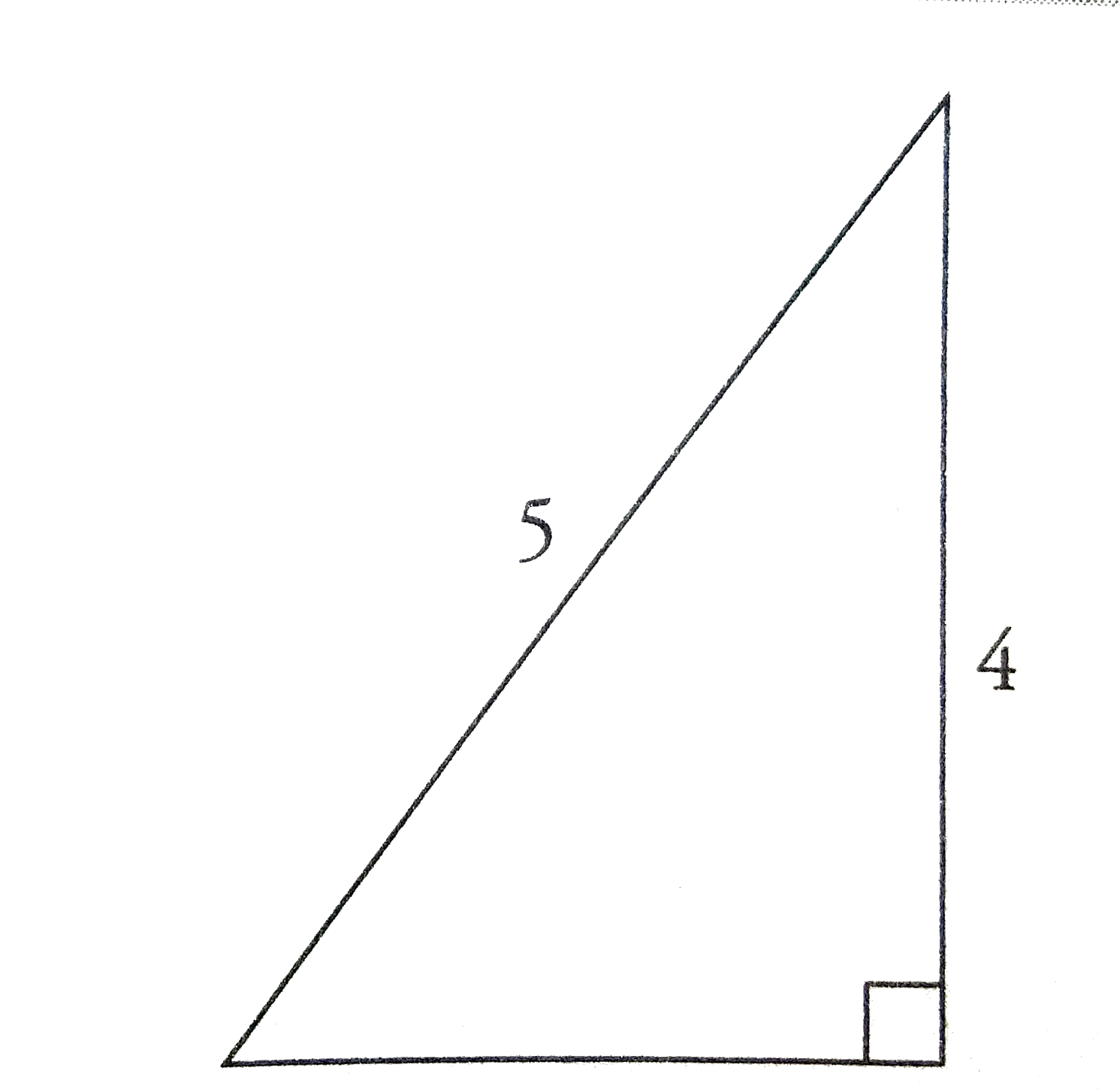
If the area of the triangle above is 6, what is its perimeter?A11B12C15D16
If Δ denotes the area of ΔABC, then b2sin2C+c2sin2B is equal to
View SolutionThe in-radius of pedal Δ of a ΔABC is
View SolutionIf Δ denote the area of any triangle with semi-perimeter , then
View SolutionIf Δ=a2−(b−c)2,Δ is the area of the ΔABC then tanA= ?
View SolutionThe area of an acute triangle ABC is Δ, the area of its pedal triangle is 'p' , where cosB=2pΔ and sinB=2√3pΔ. The value of 8(cos2AcosB+cos2C) is
View SolutionLet Δ be the area of a triangle. Find the area of a triangle whose each side is twice the side of the given triangle.
View Solution
