The in-radius of pedal $Δ$ of a $Δ A B C$ is

$\frac{R}{2}$

$R sin A sin B sin C$

$2 R cos A cos B cos C$

$4 R sin \frac{A}{2} sin \frac{b}{2} sin \frac{C}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

Updated on:21/07/2023

Answer

Step by step video & image solution for The in-radius of pedal Delta of a DeltaABC is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS PROPERTIES AND SOLUTION OF TRIANGLES

Topper's Solved these Questions

PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos

Knowledge Check

The average length of the sides of $Δ A B C$ is 12. What is the perimeter of $Δ A B C$ ?

A4
B6
C12
D36

If R be circum-radius of $a Δ,$ then circum-radius of a pedal $Δ$ is
View Solution
Let ABC be an isosceles triangle with base BC. If r is the radius of the circle inscribsed in $Δ A B C and r_{1}$ is the radius of the circle ecribed opposite to the angle A, then the product $r_{1} r$ can be equal to (where R is the radius of the circumcircle of $Δ A B C$ )
View Solution
If $s a = 4$ then area of the equilateral triangle $Δ A B C$ is equal to
View Solution
In triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of $Δ A B C$ is 96, the area of $Δ A E F$ is
View Solution
If in a $Δ A B C, A D, B E and C F$ are the altitudes and R is the circumradius, then the radius of the circumcircle of $Δ D E F$ is
View Solution
In triangle $A B C, A P : P B = 2 : 3$ . PO is parallel to BC and is P extended to Q so that CQ is parallel to BA. Find :

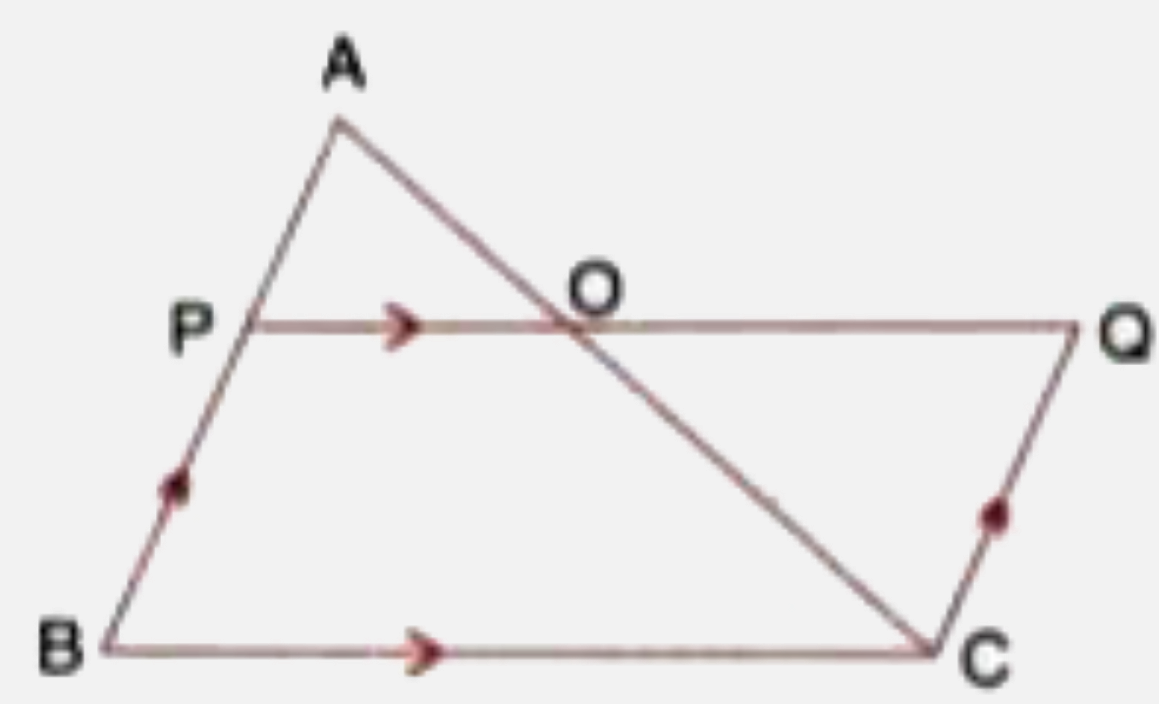
area $Δ A P O$ : area $Δ A B C$ .
View Solution
$Δ I_{1} I_{2} I_{3}$ is an excentral triangle of an equilateral triangle $Δ A B C$ such that $I_{1} I_{2} = 4$ unit, if $Δ D E F$ is pedal triangle of $Δ A B C$ , then $\frac{A r (Δ I_{1} I_{2} I_{3})}{A r (Δ D E F)} =$
View Solution

ARIHANT MATHS ENGLISH-PROPERTIES AND SOLUTION OF TRIANGLES -Exercise (Questions Asked In Previous 13 Years Exam)

The in-radius of pedal Delta of a DeltaABC is
05:46
In a triangle XYZ, let x, y, z be the lengths of sides opposite to the...
07:50
In a triangle the sum of two sides is x and the product of the same is...
04:48
Consider a triangle A B C and let a , ba n dc denote the lengths of th...
03:45
about to only mathematics
06:06
Let PQR be a triangle of area Delta with a = 2, b = 7//2, and c = 5//2...
04:29
If the angle A ,Ba n dC of a triangle are in an arithmetic propression...
04:41
Let A B C be a triangle such that /A C B=pi/6 and let a , b and c deno...
04:24
A triangle A B C with fixed base B C , the vertex A moves such that co...
04:33
Let A B Ca n dA B C ' be two non-congruent triangles with sides A B=4,...
05:24
A straight line through the vertex P of a triangle P Q R intersects th...
04:39
Consider the circle x^2 + y^2 = 9 and the parabola y^2 = 8x. They inte...
06:00
Consider the circle x^2 + y^2 = 9 and the parabola y^2 = 8x. They inte...
06:00
Consider the circle x^2 + y^2 = 9 and the parabola y^2 = 8x. They inte...
06:00
Internal bisector of /A of triangle ABC meets side BC at D. A line dra...
04:01
One angle of an isosceles triangle is 120^0 and the radius of its incr...
05:46
In Delta ABC, which one is true among the following ?
02:02
Let a vertical tower A B have its end A on the level ground. Let C be ...
04:00
ABCD is a trapezium such that AB and CD are parallel and BC bot CD. If...
07:42
For a regular polygon, let r and R be the radii of the inscribed and t...
02:30
In triangle A B C , let /c=pi/2dot If r is the inradius and R is circu...
02:32

Home
Ask Doubt
Profile

The in-radius of pedal Δ of a ΔABC is

The correct Answer is:A, B, C, D

Topper's Solved these Questions

Similar Questions

Knowledge Check

The average length of the sides of ΔABC is 12. What is the perimeter of ΔABC?

ARIHANT MATHS ENGLISH-PROPERTIES AND SOLUTION OF TRIANGLES -Exercise (Questions Asked In Previous 13 Years Exam)

The in-radius of pedal $Δ$ of a $Δ A B C$ is

The average length of the sides of $Δ A B C$ is 12. What is the perimeter of $Δ A B C$ ?