Let $f : R \to R$ be defined as $f (x) = e^{sgn x} + e^{x^{2}}$ . Then find the range of the function, and also indentify the type of the function : one-one or many-one.

Video Solution

Text Solution

Verified by Experts

$f (x) = e^{sgn x} + e^{x^{2}}$
$= ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ \begin{matrix} \frac{1}{e} + e^{x^{2}}, & x < 0 2, & x = 0 e + e^{x^{2}}, & x > 0 \end{matrix}$
For $x > 0, x^{2} > 0, e^{x^{2}} > 1 ∴ e^{x^{2}} > 1 + e$
For $x < 0, x^{2} > 0, e^{x^{2}} > 1 ∴ \frac{1}{e} + e^{x^{2}} > 1 + \frac{1}{e}$
Thus the graph of the function is as follows

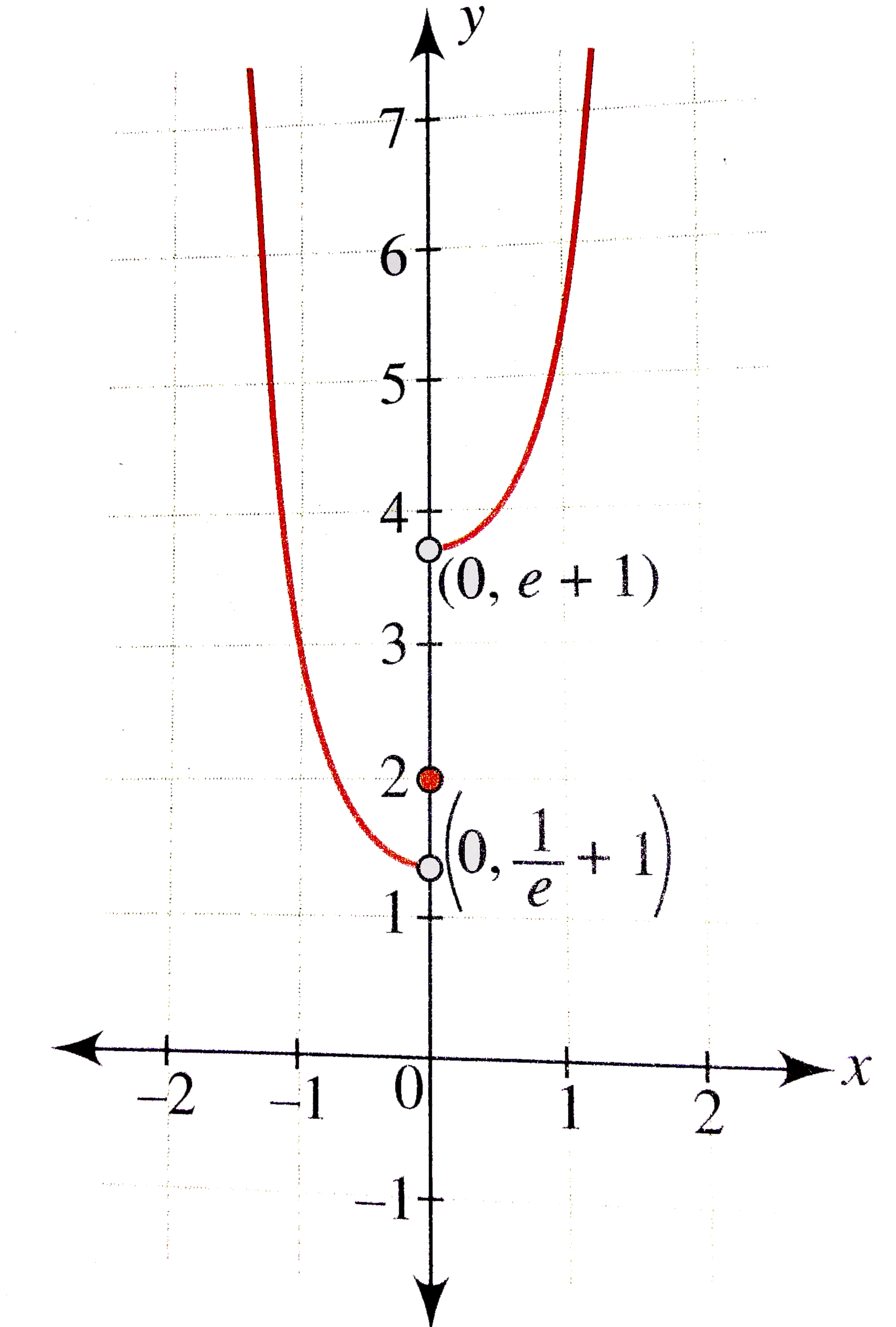
From the graph, the range of the function is $(1 + \frac{1}{e}, \infty)$ .
Also from the graph, the function is many-one.

Updated on:21/07/2023

Let $f : R \to R$ be defined as $f (x) = \frac{9 x^{2} - x + 4}{x^{2}_x + 4} .$ Then the range of the function f (x) is
A $[\frac{3}{5}, \frac{5}{3}]$
B $(\frac{3}{5}, \frac{5}{3})$
C $(- \infty, \frac{3}{5}) \cup (\frac{5}{3}, \infty)$
D $[- \frac{5}{3}, \frac{3}{5}]$
Suppose f: $R \to R$ is defined by f(x) = $\frac{x^{2}}{1 + x^{2}}$ is the range of the function? What
A(0, 1)
B(0, 1)
C(0, 1)
D(0, 1)
Let $f : R \to R$ be a function defined by $f (x) = \frac{x^{2} - 8}{x^{2} + 2}$ . Then f is
Aone-one but not onto
Bone-one and onto
Cone but not one-one
Dneither one-one nor onto