Let $f : R \to R and g : R \to R$ be respectively given by $f (x) = | x | + 1 and g (x) = x^{2} + 1$ . Define $h : R \to R$ by $h (x) = {max {f (x), g (x)}, if x \leq 0 and min {f (x), g (x)}, if x > 0$ .The number of points at which $h (x)$ is not differentiable is

Video Solution

Text Solution

Verified by Experts

First we draw the graph, of $y = | x | + 1 and y = x^{2} + 1$
$y = | x | + 1 = {\begin{matrix} x + 1, & x \geq 0 - x + 1, & x < 0 \end{matrix}$
$y = x^{2} + 1$ is a parabola having vertex at (0, 1) and concave upwards
Thus, the graphs of both functions are as shown in the following figure.

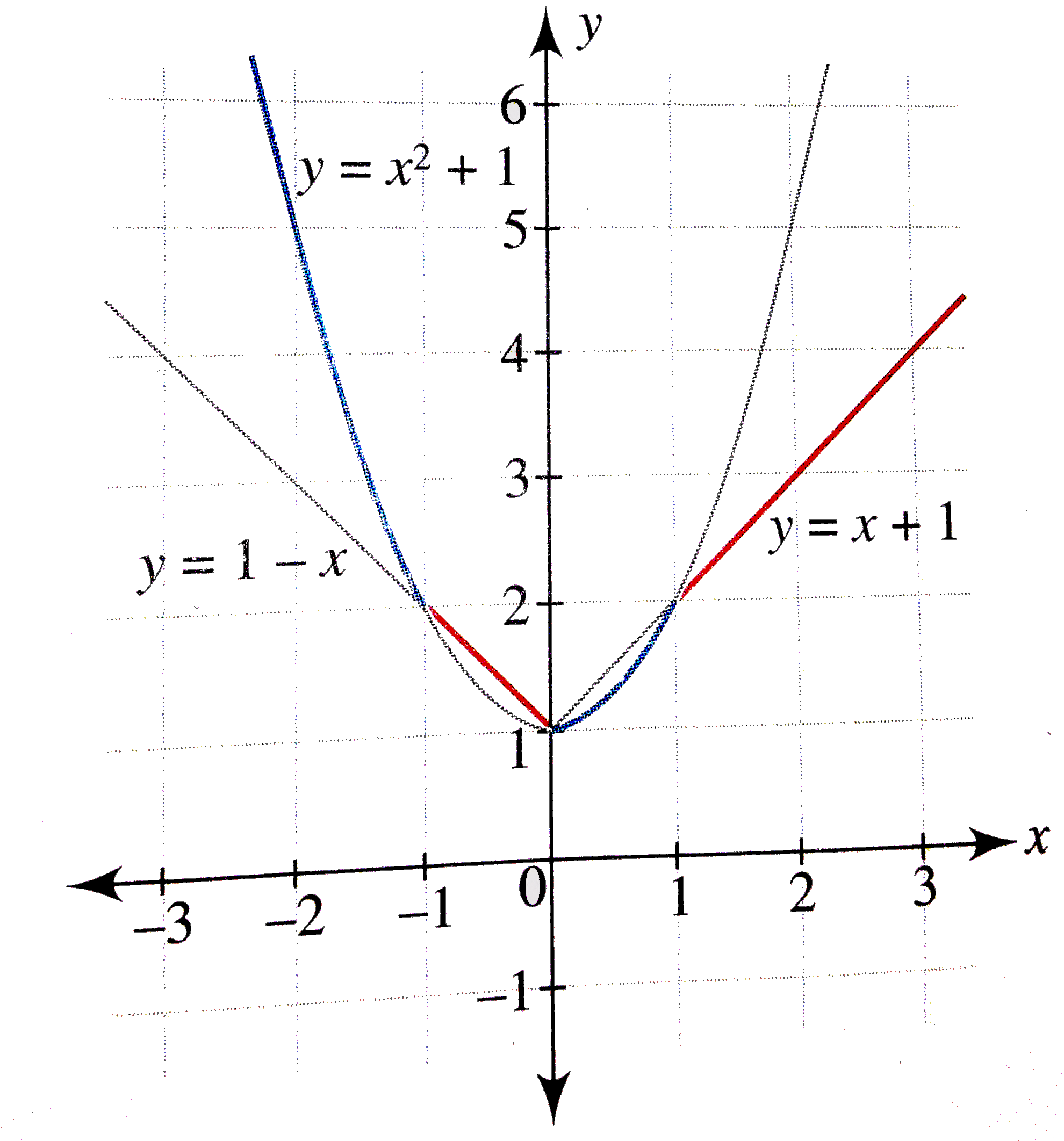
From the graph, the required function is
$h (x) = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} x^{2} + 1, & x \in (- \infty, - 1) - x + 1, & x \in [- 1, 0) x^{2} + 1, & x \in [0, 1) x + 1, & x \in [1, \infty) \end{matrix}$
which is non-different at $x = - 1, 0 and 1$ .

Updated on:21/07/2023

Let $f : R \to R and g : R \to R$ be given by $f (x) = x^{2} and g (x) = x^{3} + 1,$ then (fog) (x)
A $x^{6} + 1$
B $x^{6} - 1$
C ${(x^{3} - 1)}^{2}$
D ${(x^{3} + 1)}^{2}$
Let $f : R \to R$ and $g : R \to R$ be given by $f (x) = 3 x^{2} + 2 and g (x) = 3 x - 1$ for all $x \to R$ . Then,
A $f o g (x) = 27 x^{2} - 18 x + 5$
B $f o g (x) = 27 x^{2} + 18 x - 5$
C $g o f (x) = 9 x^{2} - 5$
D $g o f (x) = 9 x^{2} + 15$