Let f(x) be a continuous function fiven by f(x)={2x,|x|≤1x2+ax+b,|x|>1,then
If f(x) is continuous for all real x then the value of a2+b2 is
A
3
B
4
C
5
D
11
Video Solution
Text Solution
The correct Answer is:C
f(x)=⎧⎪⎨⎪⎩x2+ax+bx<−12x−1≤x≤1x2+ax+bx>1
∵ f(x)iscont∈uousatx=−1andx=1
∴ (−1)2+a(−1)+b=−2⇒b−a=−3 ...(1)
and 2=(1)2+a.1+b⇒a+b=1 ...(2)
Solving (1) and (2), we get a=2,b=−1
∴ f(x)=⎧⎪⎨⎪⎩x2+2x−1x<−12x−1≤x≤1x2+2x−1x>1
Given curves are y=f(x),x=−2y2and8x+1=0
Solving x=−2y2,y=x2+2x−1(x<−1) we get x=-2
Also, y=2x,x=−2y2 meet at (0,0)
y=2xandx=−1/8 meet at (−18,−14)
The required area is the shaded region in the figure
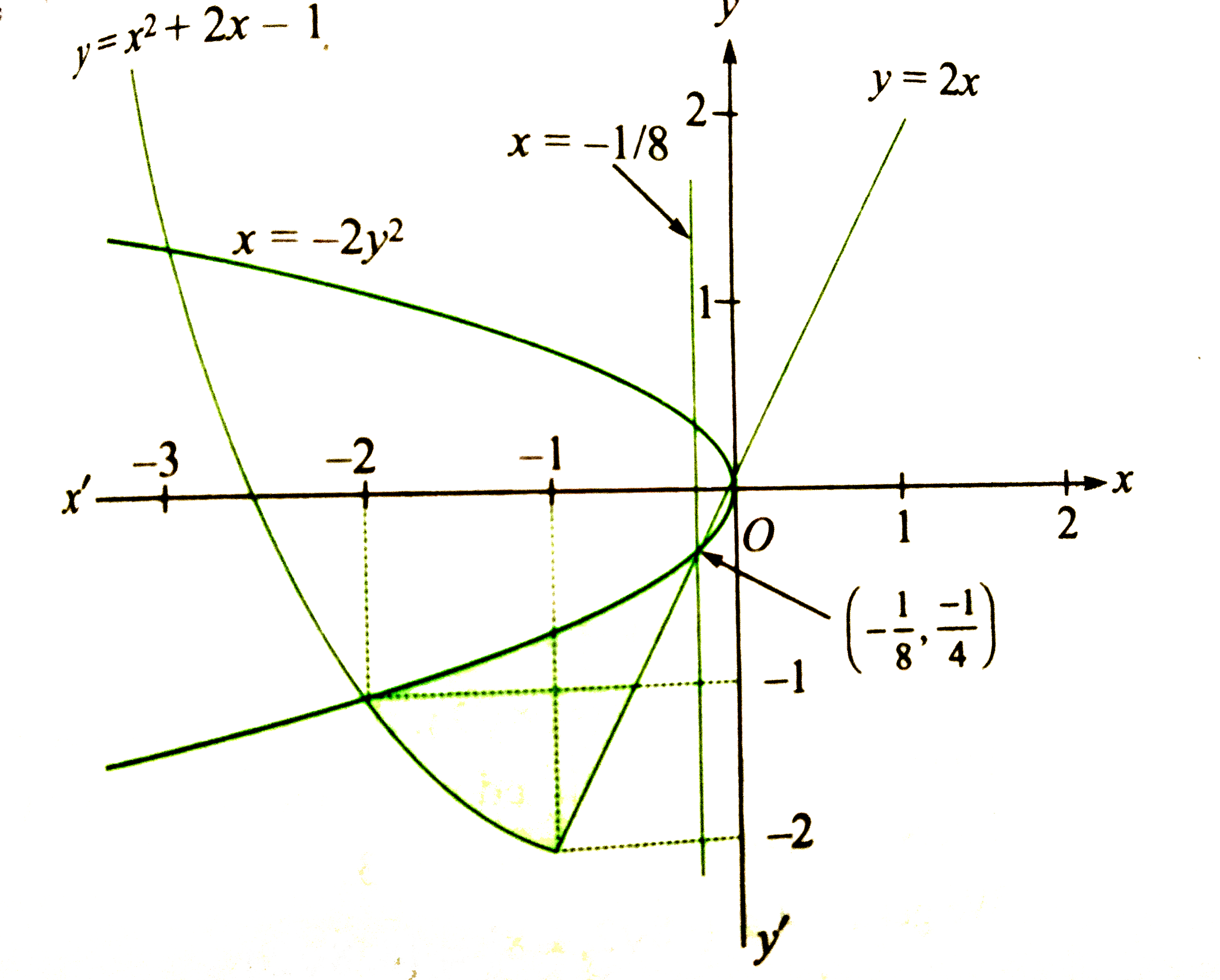
∴ Required area
=∫−1−2[−√−x2−(x2+2x−1)dx]+∫−1/8−1[−√−x2−2x]dx
=[1√22(−x)3/23−x33−x2+x]−1−2+[1√22(−x)3/23−x2]−1/8−1
=(√23+13−1−1)−(43+83−4−2)+(√23.116√2−164)−(√23−1)
=(√2−53)−(4+8−183)+(4−3192)−(√2−33)
=257192 sq. units
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)
4 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)
16 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
Let f(x)={(x+a)x<1ax2+1x≥1 then f(x) is continuous at x =1 for
Aa = 0Ba = 1CAll a∈RDNo value of aIf f(x)={ax+3,x≤2a2x−1,x>2, then the values of a for which f is continuous for all x are
Aa and -2B1 and 2C−1and2D−1and−2Let f(x)={1|x|for |x|≥1ax2+bfor |x|<1. If f(x) is continuous and differentiable everywhere, then
Aa=12,b=−32Ba=−12,b=32Ca=1, b=-1Da=b=1
If the function f(x) given by f(x)=⎧⎪⎨⎪⎩3ax+bif x>111if x=15ax−2bif x<1 is continuous at x=1 then find the values of aandb.
View SolutionIf the function f:R→R given by
f(x)={x+a,if x≤13−x2,if x>1 is continuous at x = 1, then a is equal to
View SolutionLet f(x)={x+1,x≤13−ax2,x>1 The value of a so that f is continuous is
View SolutionIf f(x)={2x+1,x≤1−3−kx2,x>1 is continuous at x = 1, then the value of k is
View SolutionIf the function f:R→R given by f(x)={x+aif x≤13−x2if x>1 is continuous at x=1, then a is equal to
View Solution
