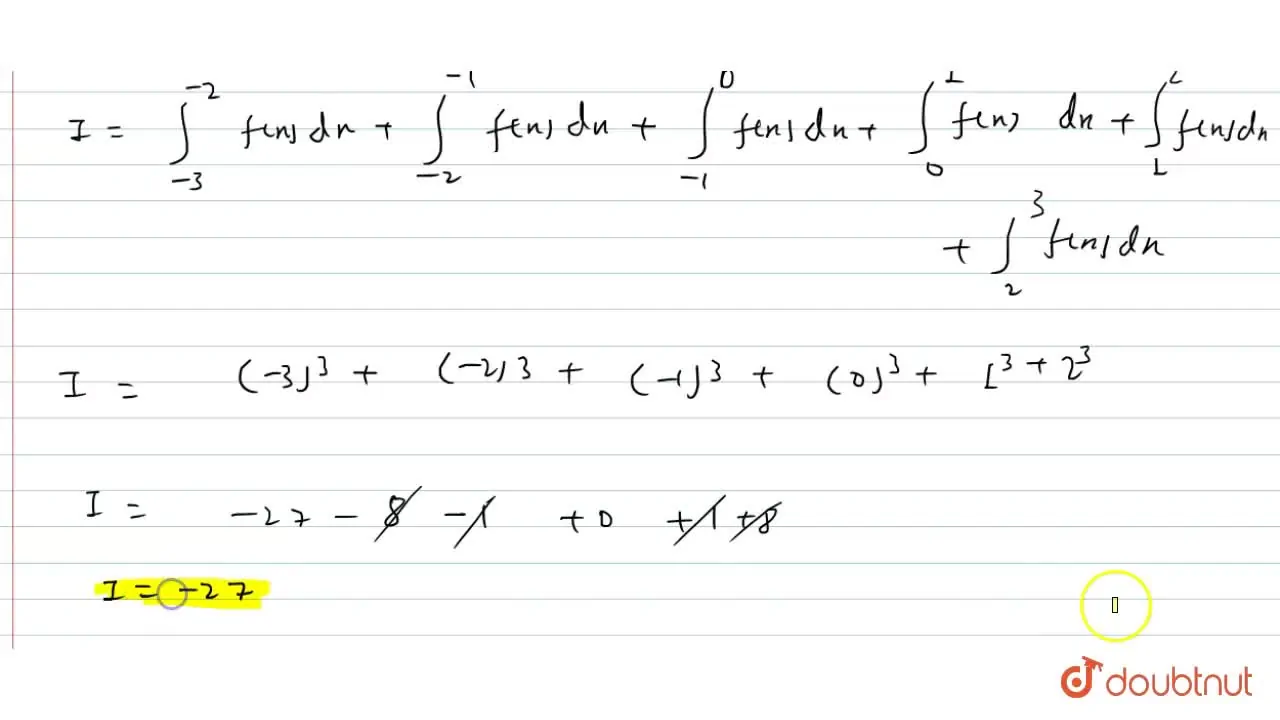Let f(x) be a continuous function such that ∫n+1nf(x)dx=n3,n∈Z. Then the value of the integeral ∫3−3f(x) dx, is
9
−27
−9
none of these
The correct Answer is:B
We have,
3∫−3f(x)−5∑r=0−3+r+1∫−3+rf(x)dx
⇒3∫−3f(x)dx−5∑r=0(−3+r)3⎡⎢⎣∴n+1∫nf(x)dx=n3⎤⎥⎦
3∫−3f(x)dx=[(−3)3+(−2)3+(−1)3+02+13+23]=−27
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Section II - Assertion Reason Type12videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Exercise147videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise26videos
DERIVATIVE AS A RATE MEASURER
Similar Questions
Let f(x) be a contiuous function such a ∫n+1nf(x)dx=n3,n∈Z. Then, the value of the intergral ∫3−3f(x)dx (A) 9 (B) −27 (C) −9 (D) none of these
View SolutionLet f(x) be a continuous function and I=∫91√xf(x)dx, then
View SolutionLet f(x) be a continuous function such that f(a-x)+f(x)=0 for all x∈[0,a]. Then, the value of the integral
∫a011+ef(x)dx is equal toView SolutionIf f(x) is a continuous function satisfying f(x)=f(2−x), then the value of the integral I=∫3−3f(1+x)ln(2+x2−x)dxis equal to
View SolutionIf for every integer n,∫n+1nf(x)dx=n2, then the value of ∫4−2f(x)dx is
View SolutionIf f(x) is continuous and ∫90f(x)dx=4, then the value of the integral ∫30x.f(x2)dx is
View SolutionLet f be a periodic continuous function with period T>0. If I=∫T0f(x)dx Then the value of I1=∫4+4T4f(3x)dx is
View SolutionLet T>0 be a fixed real number. Suppose f is continuous function such that for all x∈R,f(x+T)=f(x). If I=∫T0f(x)dx, then the value of ∫3+3T3f(2x)dx is 32I (b) 2I (c) 3I (d) 6I
View SolutionLet f(x) be a non-negative continuous function defined on R such that f(x)+f(x+12)=3 , then the value of 11008∫20150f(x)dx is
View SolutionLet f:R→R be continuous function such that f(x)=f(2x) for all x∈R. If f(t)=3, then the value of ∫1−1f(f(x))dx, is
View Solution