Let f(x)=x+2|x+1|+x−1∣.Iff(x)=k has exactly one real solution, then the value of k is3 (b) 0 (c) 1(d) 2
3
0
1
2
The correct Answer is:A
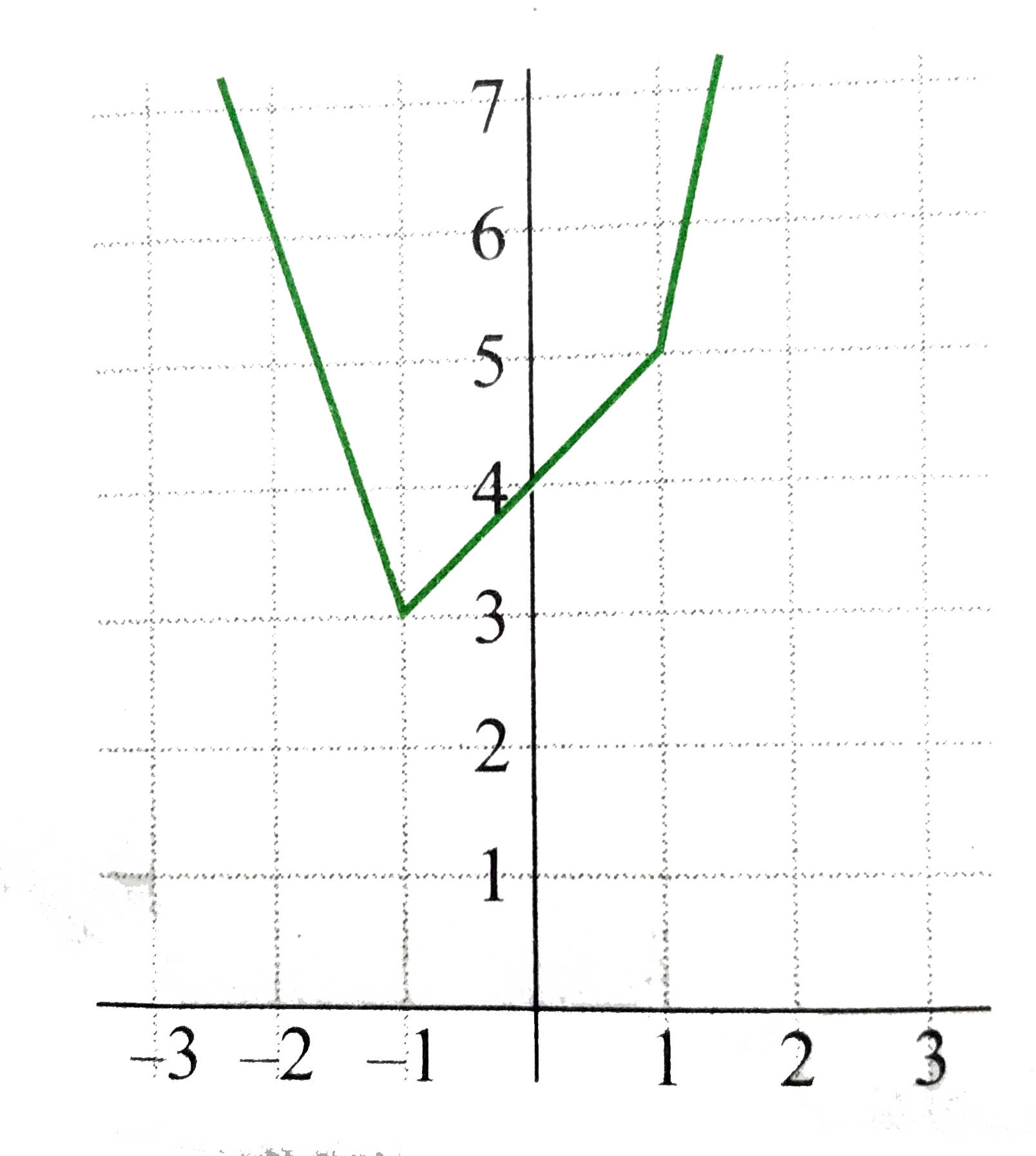
Let f(x)=x+2|x+1|+2|x−1|
=⎧⎪⎨⎪⎩x−2(x+1)−2(x−1),x<−1x+2(x+1)−2(x−1),−1≤x≤1x+2(x+1)+2(x−1),x>1
=⎧⎪⎨⎪⎩−3x,x<−1x+4,−1≤x≤15x,x>1
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Multiple)27videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)32videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.158videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank31videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
Let f(x)=x+2|x+1|+2|x−1|. If f(x)=k has exactly one real solution, then the value of k is (a)3 (b) 0 (c)1 (d) 2
View SolutionLet f(x)=||x−1|+a|−4,iff(x)=0 has three real solution, then the values of lies in
View SolutionLet f(x)=[2+x,,x≥0,4−x,,x<0,If f(f(x))=k has at least one solution,then smallest value of k is
View SolutionLet f(x)=x+2|x+1|+2|x−1|. Find the values of k if f(x)=k
(i) has exactly one real solution,
(ii) has two negative solutions,
(iii) has two solutions of opposite sign.View SolutionLet f(x)=2+x,x≥0 and f(x)=4−x,x<0 if f(f(x))=k has at least one solution, then smallest value of k is
View SolutionLet f(x)=exx2 x∈R−{0}. If f(x) = k has two distinct real roots, then the range of k, is
View SolutionLet f(x)=x3−3x2+2x . If the equation f(x)=k has exactly one positive and one negative solution then the value of k equals. −2√39 (b) −29 23√3 (d) 13√3
View SolutionLetf(x)=min{ex,32,1+e−x} if f(x)=k has at least 2 solutions then k can not be
View SolutionIf x2+5x−2k, is exactly divisible by (x-1), then the value of K is
(A) 1 (B) 2 (C ) 3 (D) 4View SolutionNumber of real values of k for which the equation x+2kx−1=x has exactly one real solution is (A) 0 (B) 1 (C) 2 (D) 3
View Solution

