Question

Let $f\left(x\right)=x+2|x+1|+2|x-1|$. Find the values of $k$ if $f\left(x\right)=k$
(i) has exactly one real solution,
(ii) has two negative solutions,
(iii) has two solutions of opposite sign.

Explanation

Let `f(x)= x+2 |x+1|+2|x-1|`
`y= f(x)` changes definition at `x=-1 and x=1`.
Since the graph of the function is a straight line in each region `(-oo, -1), (-1, 1) and (1, oo)`, we need to check the values at some particular values of x to draw the graphs.
`" "f(-2)= -2+2(1)+2(3)=6`
`" "f(-1)= -1+ 2(0)+ 2(2)=3`
`" "f(1)= 1+2(2)+ 2(0)=5`
`" "f(2)= 2+2(3)+ 2(1)=10`
Thus, we plot the points `(-2, 6), (-1, 3), (1, 5) and (2, 10)`.
Plotting these points and connecting with the straight line, we have the following graph.

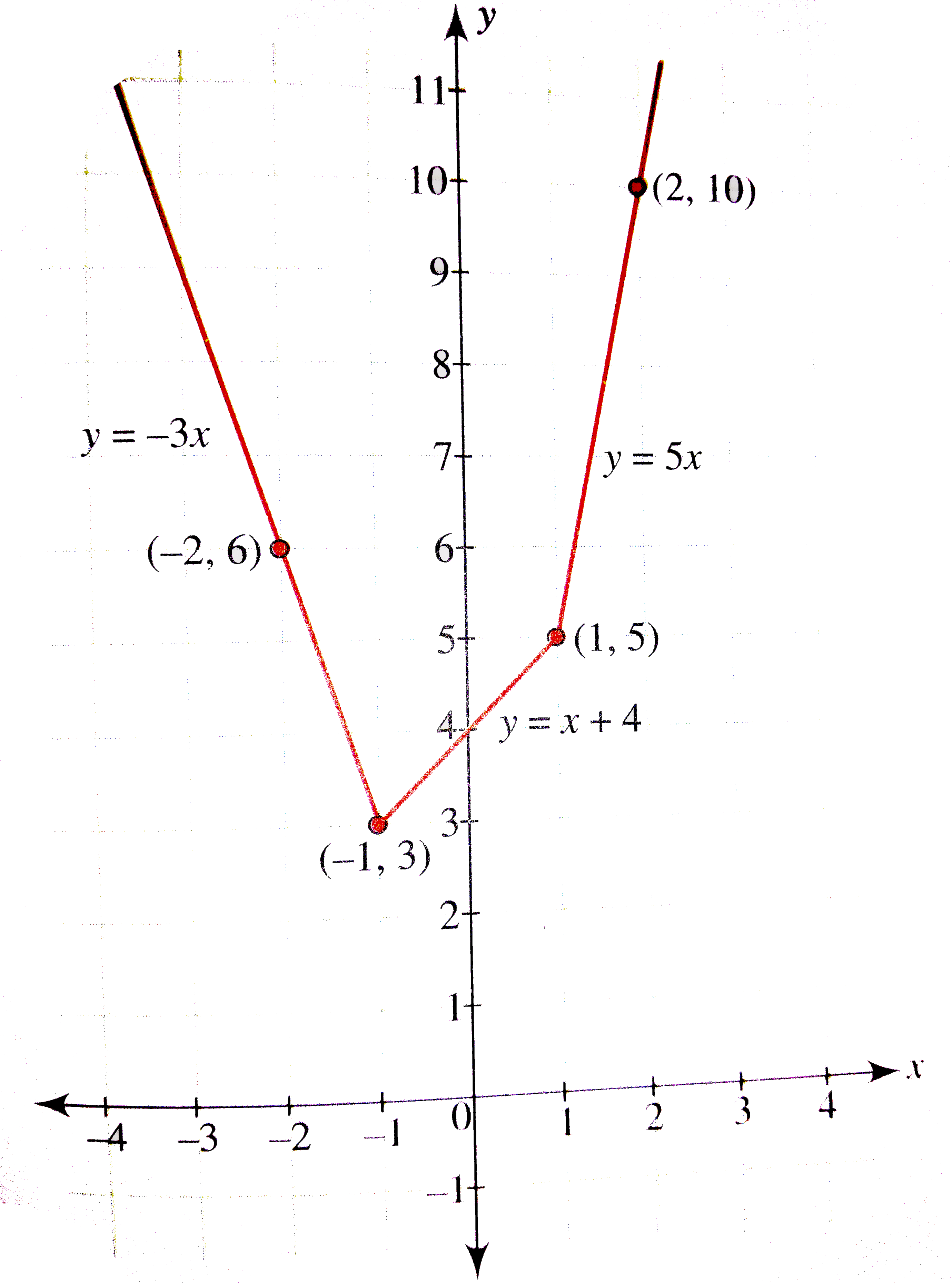
For the equation `f(x)=k` to have exactly one real root, the line y =k must intersect the graph of `y= f(x)` at the point `(-1, 3)`, hence the value of `k` is 3.
For the equation `f(x)=k ` to have two negative real roots, the line `y=k` must intersect the graph of `y=f(x)` at the point between `y=3 and y=4`, hence the values of k are `(3, 4)`.
For the equation `f(x)= k` to have real roots of opposite sign, the line `y=k` must intersect the graph of `y=f(x)` above `y=4`, hence the values of `k` are `(4, oo)`.