Let I be the purchase value of an equipment and V(t) be the value after it has been used for t years. The value V(t) depreciates at a rate given by differential equation dV(t)dt=-k(T-t) , where k>0 is a constant and T is the total life in years of the equipment. Then the scrap value V(T) of the equipment is : (1) T2−1k (2) I−kT22 (3) I−k(T−t)22 (4) e−kT
T2−Ik
I−kT22
I−(T−t)22
e−kT
The correct Answer is:D
We have,
dVdt=−k(T−t)
⇒ dV=−k(T−t)dt
On integrating, we get
∫dV=−k∫(T−t)dt
⇒ V(t)=k(T−t)22+C …(i)
Initially i.e. at t = 0, we have V(t) = I. Putting t = 0 and V (t) = I in (i), we get
∴ I=kT22+C⇒C=I−kT22
Putting this value of C in (i), we get
V(t)=k(T−t)22+I−kT22
At t = T, we get
V(T)=I−kT22
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Section II - Assertion Reason Type
5 Videos
- DIFFERENTIAL EQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Exercise
74 Videos
- DIFFERENTIAL EQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Chapter Test
30 Videos
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26 Videos
- DIFFERENTIALS, ERRORS AND APPROXIMATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIALS, ERRORS AND APPROXIMATIONSEXERCISE - Exercise
17 Videos
Similar Questions
V=k(PT)0.33 where k is constant. It is an,
View SolutionIf t>0 and t2−4=0, what is the value of t ?
View SolutionIf currentI=Kcosωt+Ksinωt, (where K is a constant and t is time), then RMS value of current for one complete cycle is
View SolutionIf i=t2,0<t<T then r.m.s. value of current is
View SolutionThe instantaneous velocity of a particle moving in a straight line is given as a function of time by: v=v0(1−(tt0)n) where t0 is a constant and n is a positive integer . The average velocity of the particle between t=0 and t=t0 is 3v04.Then , the value of n is
View SolutionIf the sum of the zeros of the quadratic polynomial f(t)=kt2+2t+3k is equal to their product, find the value of k.
View SolutionThe x-t equation is given as x=2t+1. The corresponding v-t graph is
View SolutionFind the aveage for the saw-tooth voltage of peak value V0 from t=0 to t=2T as shown in figure.
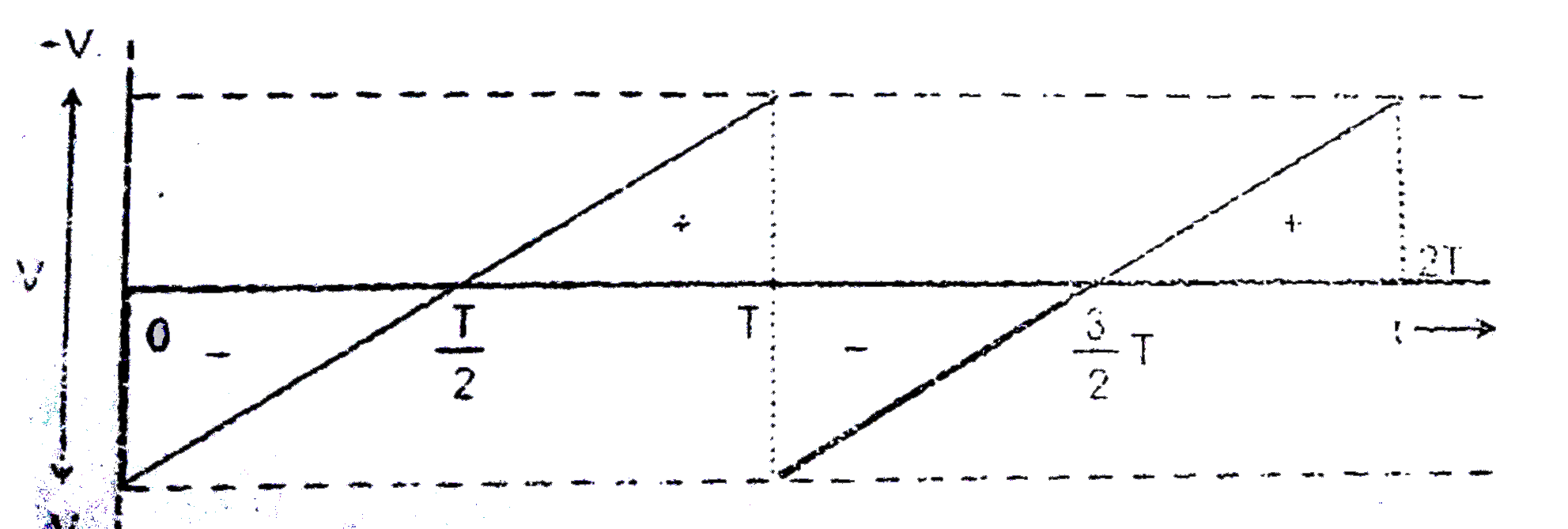
View SolutionIf velocity v varies with time t as v=2t2, then the plot between v and t2 will be given as :
View SolutionIf velocity v varies with time t as v=2t2, then the plot between v and t2 will be given as :
View Solution
