Let 'l' is the length of median from the vertex A to the side BC of a . Then
The correct Answer is:A, B, C, D
D is the midpoint of BC

Using Apollonius theorem, we have
(where AD = l)
Also
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type6videos
SOLUTIONS AND PROPERTIES OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type6videos
SOLUTIONS AND PROPERTIES OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Archives1videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - STATISTICSEXERCISE - Archives10videos
STATISTICS
Similar Questions
In ΔABC,'h' is the length of altitude drawn from vertex A on the side BC. Prove that:
2(b2+c2)≥4h2+a2. Also, discuss the case when equality holds true.View SolutionTwo sides of a triangle are to have lengths 'a'cm & 'b'cm. If the triangle is to have the maximum area, then the length of the median from the vertex containing the sides 'a' and 'b'is
View SolutionLet the lengths of the altitudes drawn from the vertices of ΔABC to the opposite sides are 2, 2 and 3. If the area of ΔABC is Δ, then find the area of triangle
View SolutionLet position vectors of point A,B and C of triangle ABC represents be ˆi+ˆj+2ˆk,ˆi+2ˆj+ˆk and 2ˆi+ˆj+ˆk. Let l1,l2 and l3 be the length of perpendicular drawn from the orthocenter 'O' on the sides AB, BC and CA, then (l1+l2+l3) equals
View SolutionLet position vectors of point A,B and C of triangle ABC represents be ˆi+ˆj+2ˆk,ˆi+2ˆj+ˆk and 2ˆi+ˆj+ˆk. Let l1+l2 and l3 be the length of perpendicular drawn from the orthocenter 'O' on the sides AB, BC and CA, then (l1+l2+l3) equals
View SolutionThe slope of a median, drawn from the vertex A of the triangle ABC is -2. The co-ordinates of vertices B and C are respectively (-1, 3) and (3, 5). If the area of the triangle be 5 square units, then possible distance of vertex A from the origin is/are.
View SolutionFind the length of side BC in the given triangle.
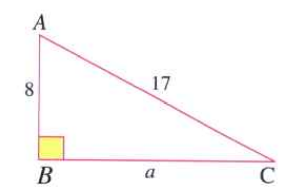 View Solution
View SolutionLet f,gandh be the lengths of the perpendiculars from the circumcenter of ΔABC on the sides a, b, and c, respectively. Prove that af+bg+ch=14abcfgh
View SolutionIf in ΔABC,b=3cm,c=4cm and the length of the perpendicular from A to the side BC is 2 cm, then how many such triangle are possible ?
View SolutionIn a !ABC the length of the median AD to the side BC is 4 units. If ∠A=60∘ and the area of the triangle is 2√3 sq. units. The length of side BC, is
View Solution


