In a !ABC the length of the median AD to the side BC is 4 units. If ∠A=60∘ and the area of the triangle is 2√3 sq. units. The length of side BC, is
2√3
4√3
6
8
To find the length of side BC in triangle ABC given the median AD, angle A, and the area of the triangle, we can follow these steps:
Step 1: Use the area formula of a triangle
The area of triangle ABC can be expressed using the formula:
Area=12×BC×sinA
Given that the area is 2√3 square units and ∠A=60∘, we can substitute these values into the formula:
2√3=12×BC×sin(60∘)
Step 2: Substitute the value of sin(60∘)
We know that sin(60∘)=√32. Substituting this into the equation gives:
2√3=12×BC×√32
Step 3: Simplify the equation
This simplifies to:
2√3=BC⋅√34
Multiplying both sides by 4 to eliminate the fraction:
8√3=BC⋅√3
Step 4: Divide both sides by √3
BC=8
Step 5: Conclusion
Thus, the length of side BC is 8 units.
The area of triangle ABC can be expressed using the formula:
Area=12×BC×sinA
Given that the area is 2√3 square units and ∠A=60∘, we can substitute these values into the formula:
2√3=12×BC×sin(60∘)
We know that sin(60∘)=√32. Substituting this into the equation gives:
2√3=12×BC×√32
This simplifies to:
2√3=BC⋅√34
Multiplying both sides by 4 to eliminate the fraction:
8√3=BC⋅√3
BC=8
Thus, the length of side BC is 8 units.
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - SOLVED MCQ
2 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
Similar Questions
Knowledge Check
In triangle ABC, AB = 5 and AC = 3. which one of the following is the measure of the length of side BC?
ABC<7BBC=7CBC>7DIt cannot be determined from the information given
In a ΔABC, the median to the side BC is of length 1√11−6√3 and it divides the ∠A into angles 30∘ and 45∘. Find the length of the side BC.
View SolutionIn a ΔABC, the median to the side BC is of length 1√11−6√3 and it divides the ∠A into angles 30∘ and 45∘. Find the length of the side BC.
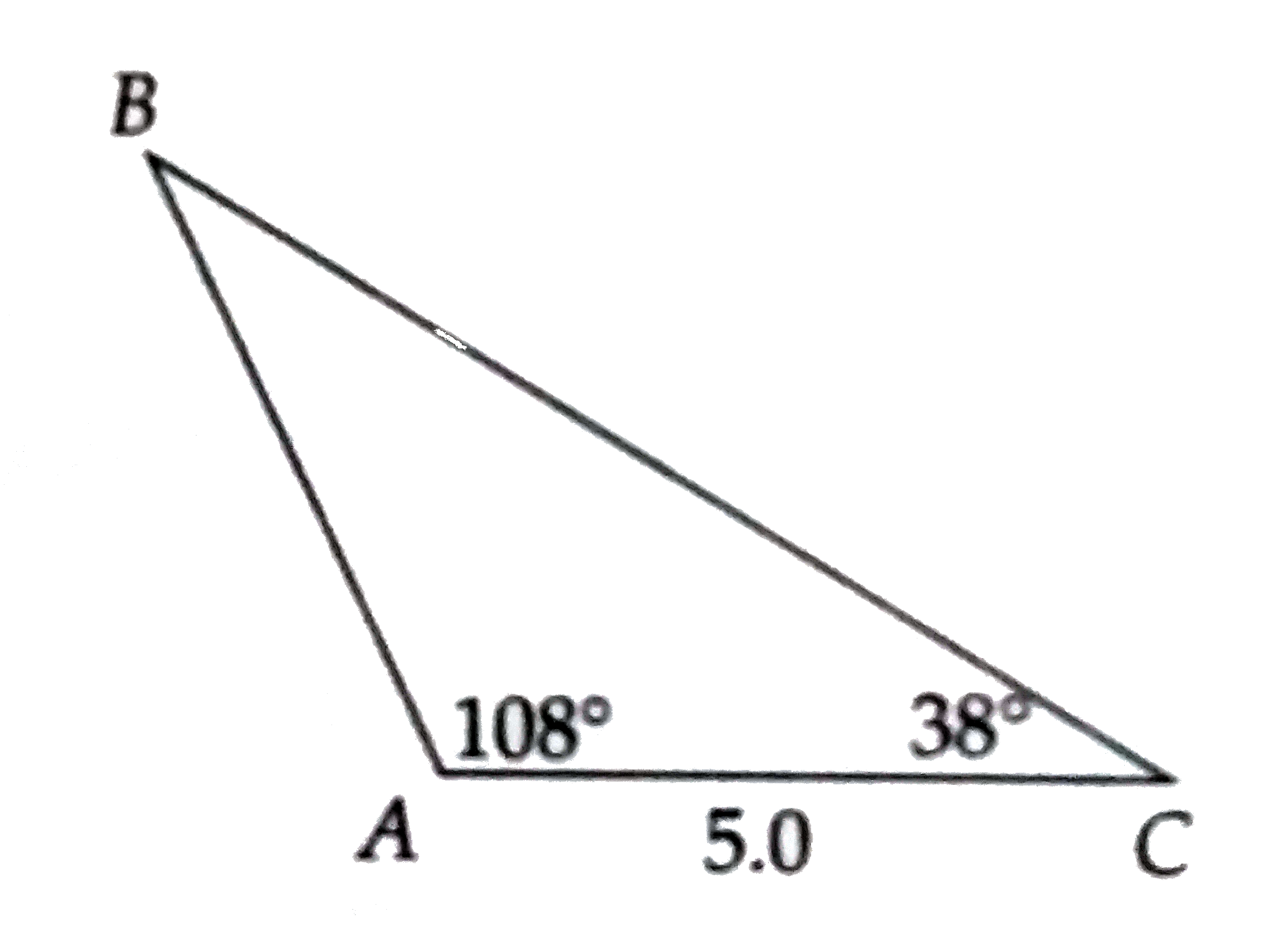
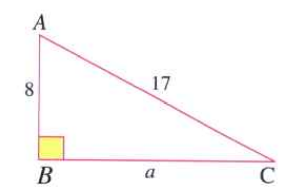
View SolutionFind the length of side BC in the given triangle.
View SolutionTwo medians drawn from the acute angles of a right angled triangle intersect at an angle π6. If the length of the hypotenuse of the triangle is 3 units, then the area of the triangle (in sq. units) is (a) √3 (b) 3 (c) √2 (d) 9
View SolutionLet 'l' is the length of median from the vertex A to the side BC of a ΔABC. Then
View SolutionABCD is a parallelogram. x + 2y = 3 and 2x + y = 3 are the equations of the diagonals AC and BD respectively. AC = 4 units and area of parallelogram ABCD is 8 sq. units then The length of BC is equal to
View SolutionThe area of a triangle is √3 sq. units and ∠B=60 If a2,b2,c2 are in A.P., the length of side AC is
View Solution