Let P be a point inside a triangle ABC with ∠ABC=90∘ . Let P1andP2 be the images of P under reflection in AB and BC respectively. The distance between the circumcenters of triangles ABC and P1P2 is
AB2
AP+BP+CP3
AC2
AB+BC+AC2
The correct Answer is:c
M is circumcentre of ΔABC
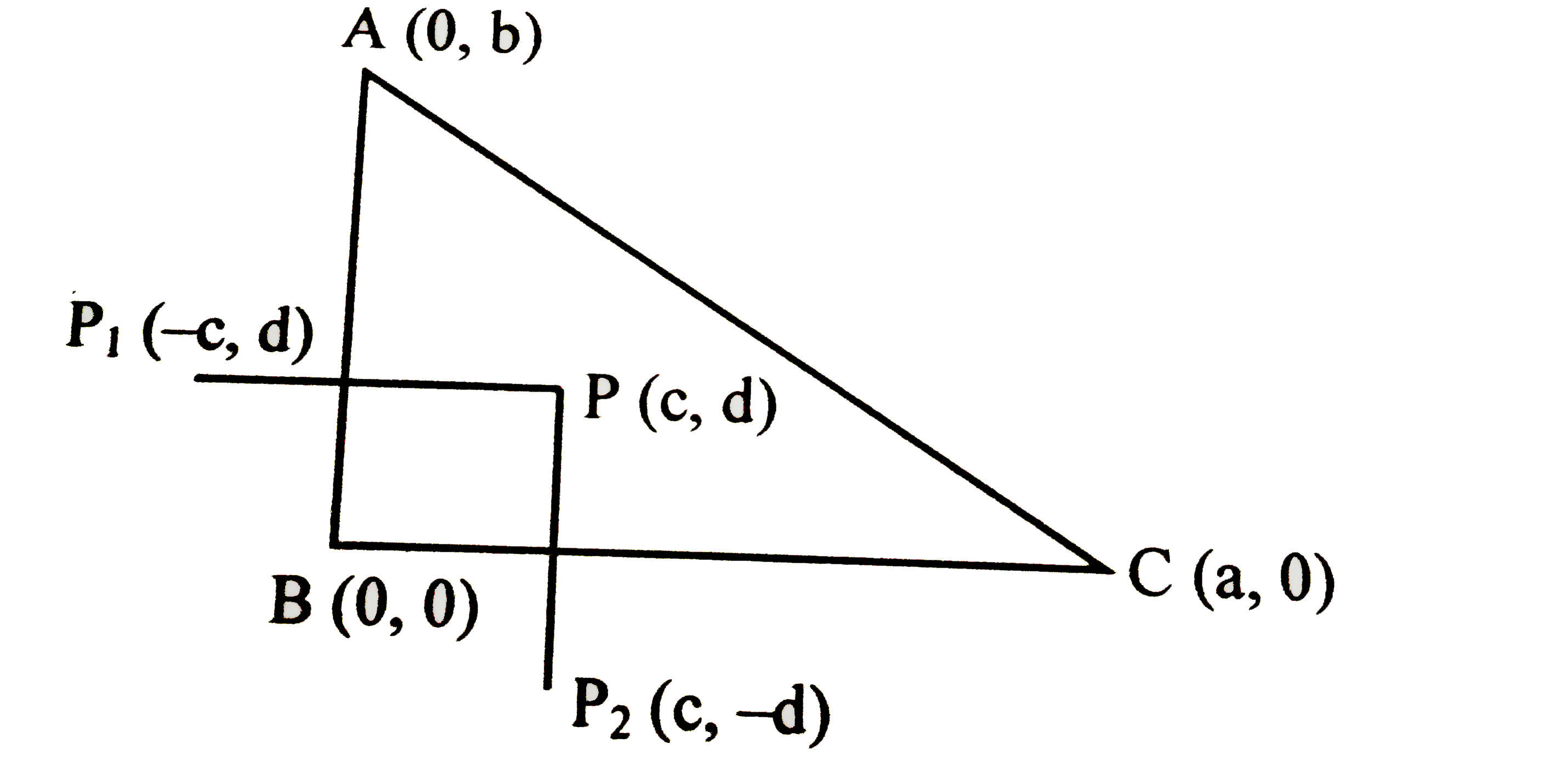
M(a2b2)
M is circumcetre of ΔABC
N= (0,0) = B ( mid- point of p1&P2)
so MN AC2
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 1 Mathematics
45 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - exercise
18 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 2 Mathematics
15 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Knowledge Check
Let P be an interior point of a triangle ABC , Let Q and R be the reflections of P in AB and AC , respectively if Q .A , R are collinear then ∠A equals -
A30∘B60∘C90∘D120∘If in a △ABC,a,b,c are in A.P. and P1,P2,P3 are th altitude from the vertices A,B and Crespectively then
AP1,P2,P3 are in A.P.BP1,P2,P3 are in H.P.CP1+P2+P3≤3R△D1P1+1P2+1P3≤3R△In right angled ΔABC,∠B=90∘, if P and Q are points on the sides AB and BC respectively, then :
 AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)
AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)
If P1,P2 and P3 are the altitudes of a triangle from vertices A,B and C respectively and Δ is the area of the triangle, then the value of 1P1+1P2−1P3=
View SolutionIf the angles of a triangle ABC are in A.P., then
View SolutionIf I is the incenter of the circle inscribed in the triangle ABC and AI cuts BC at P, then
View SolutionIn a triangle ABC, points P, Q and R are the mid-points of the sides AB, BC and CA respectively. If the area of the triangle ABC is 20 sq. units, find the area of the triangle PQR
View SolutionA circle is inscribed in a triangle ABC. It touches the sides AB, BC and AC at the points R, P and Q respectively. If AQ = 4.5 cm, PC = 5.5 cm and BR = 6 cm, then the perimeter of the triangle ABC is:
एक वृत्त किसी त्रिभुज ABC में अन्तर्निहित है | यह भुजाओं AB, BC और AC को क्रमशः बिंदु R, P और Q पर स्पर्श करता है | यदि AQ = 4.5 सेमी, PC = 5.5 सेमी और BR = 6 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View Solution
