Let Pn(ix)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
0
n
1
n+1
The correct Answer is:A
To solve the problem, we need to analyze the polynomial Pn(x)=1+2x+3x2+…+(n+1)xn where n is even, and determine the number of real roots of the equation Pn(x)=0.
Step 1: Understand the Polynomial
The polynomial Pn(x) is defined as:
Pn(x)=1+2x+3x2+…+(n+1)xn
where n is an even integer.
Step 2: Evaluate the Polynomial at Specific Points
Let's evaluate Pn(x) at x=0:
Pn(0)=1+2(0)+3(0)2+…+(n+1)(0)n=1
This shows that Pn(0)=1, which is positive.
Step 3: Analyze the Behavior of the Polynomial for x>0
For x>0, all terms in the polynomial are positive:
Pn(x)=1+2x+3x2+…+(n+1)xn>0
Thus, Pn(x)>0 for all x>0.
Step 4: Analyze the Behavior of the Polynomial for x<0
Now, consider x<0. Since n is even, the leading term (n+1)xn will be positive as xn will be positive when n is even. The polynomial can be expressed as:
Pn(x)=1+2x+3x2+…+(n+1)xn
As x approaches negative infinity, the leading term dominates:
Pn(x)→+∞ as x→−∞
Step 5: Check for Roots in the Interval (−∞,0)
To find the number of real roots, we need to check if Pn(x) can cross the x-axis in the interval (−∞,0). Since Pn(0)=1>0 and Pn(x)→+∞ as x→−∞, we need to check if there are any points where Pn(x) could be negative.
Step 6: Conclusion
Since Pn(x) is continuous and starts at a positive value at x=0 and goes to positive infinity as x→−∞, and because all terms contribute positively for x>0, we conclude that:
- Pn(x) does not cross the x-axis.
- Therefore, there are no real roots.
Thus, the number of real roots of Pn(x)=0 is:
0
The polynomial Pn(x) is defined as:
Pn(x)=1+2x+3x2+…+(n+1)xn
where n is an even integer.
Let's evaluate Pn(x) at x=0:
Pn(0)=1+2(0)+3(0)2+…+(n+1)(0)n=1
This shows that Pn(0)=1, which is positive.
For x>0, all terms in the polynomial are positive:
Pn(x)=1+2x+3x2+…+(n+1)xn>0
Thus, Pn(x)>0 for all x>0.
Now, consider x<0. Since n is even, the leading term (n+1)xn will be positive as xn will be positive when n is even. The polynomial can be expressed as:
Pn(x)=1+2x+3x2+…+(n+1)xn
As x approaches negative infinity, the leading term dominates:
Pn(x)→+∞ as x→−∞
To find the number of real roots, we need to check if Pn(x) can cross the x-axis in the interval (−∞,0). Since Pn(0)=1>0 and Pn(x)→+∞ as x→−∞, we need to check if there are any points where Pn(x) could be negative.
Since Pn(x) is continuous and starts at a positive value at x=0 and goes to positive infinity as x→−∞, and because all terms contribute positively for x>0, we conclude that:
- Pn(x) does not cross the x-axis.
- Therefore, there are no real roots.
0
Topper's Solved these Questions
- MISCELLANEOUS EQUATIONS AND INEQUATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Exercise
30 Videos
- MEASURES OF CENTRAL TENDENCYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test
21 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
Similar Questions
Let Pn(x)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
View SolutionThe maximum number of real roots of the equation x2n−1=0, is
View SolutionLet p(x) = a0+a1x+a2x2+.............+anxn be a non zero polynomial with integer coefficient . if p(√2+√3+√6)=0 , the smallest possible value of n . is
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
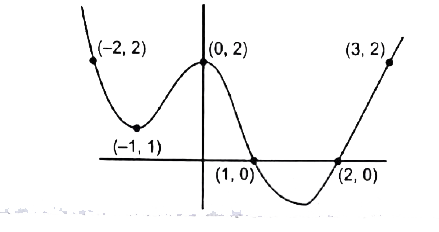
The minimum number of real roots of equation (p'(x))2+p(x)p''(x)=0 are:
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
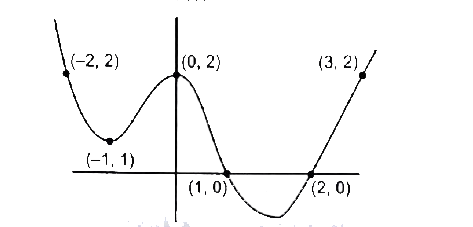
The product of all imaginary roots of p(x)=0 is:
View SolutionLet n be a positive integer with f(n)=1!+2!+3!+.........+n!andp(x),Q(x) be polynomial in x such that f(n+2)=P(n)f(n+1)+Q(n)f(n) for all n≥, Then
View SolutionLet f(x)=(x+1)(x+2)(x+3)…..(x+100)andg(x)=f(x)f''(x)−f'(x)2. Let n be the numbers of real roots of g(x)=0, then:
View SolutionLet Pn(u) be a polynomial is u of degree n. Then, for every positive integern, sin2nx is expressible is
View SolutionIf the polynomial equation anxn+an−1xn−1+an−2xn−2+.......+a0=0,n being a positive integer, has two different real roots a and b. then between a and b the equation nanxn−1+(n−1)an−1xn−2+.......+a1=0 has
View SolutionIf a is defined by f (x)=a0xn+a1xn−2+a2xn−2+...+an−1x+an where n is a non negative integer and a0,a1,a2,…….,an are real numbers and a0≠0, then f is called a polynomial function of degree n. For polynomials we can define the following theorem
(i) Remainder theorem: Let p(x) be any polynomial of degree greater than or equal to one and 'a' be a real number. if p(x) is divided by (x-a), then the remainder is equal to p(a).
(ii) Factor theorem : Let p(x) be a polynomial of degree greater than or equal to 1 and 'a' be a real number such that p(a) = 0, then (x-a) is a factor of p(x). Conversely, if (x-a) is a factor of p(x). then p(a)=0.
The number of real roots of the equation, (x−1)2+(x−2)2+(x−3)2=0 is
View Solution
