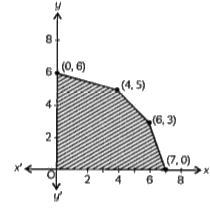
Let R be the feasible region (convex polygon) for a linear programming problem and Z = ax + by be the objective function. Then, which of the following statements is false? A) When Z has an optimal value, where the variables x and y are subject to constraints described by linear inequalities, this optimal value must occur at a corner point (vertex) of the feasible region . B)If R is bounded, then the objective function Z has both a maximum and a minimum value on Rand each of these occurs at a corner point of R . C) If R is unbounded, then a maximum or a minimum value of the objective function may not exist D) If R is unbounded and a maximum or a minimum value of the objective function z exists, it must occur at corner point of R
When Z has an optimal value, where the variables x and y are subject to constraints described by linear inequalities, this optimal value must occur at a corner point (vertex) of the feasible region .
If R is bounded, then the objective function Z has both a maximum and a minimum value on Rand each of these occurs at a corner point of R .
If R is unbounded, then a maximum or a minimum value of the objective function may not exist
If R is unbounded and a maxil'TUJm or a minimum value of the objective function z exists, it must occur at corner point of R
The correct Answer is:D
If the feasible region is unbounded and the maximum or a minimum value of Z exists, it must occur at a corner point of R.
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner13videos
Linear Programming
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )15videos
Linear Programming
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner3videos
LINE
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER22videos
MATHEMATICAL LOGIC
Similar Questions
Knowledge Check
- Question 1 - Select One
One of the corner points of the feasible region of inequalities gives
AOptimal solution of LPPBObjective functionCConstraintsDLinear assumptions - Question 2 - Select One
The optimal value of the objective function is attained at the points
Agiven by intersectionn of inequations with axis onlyBgiven by intersection of inequations with X-axis onlyCgiven by corner points of the feasible regionDnone of the above - Question 3 - Select One
The optimal value of the objective function is attained at the points
Agiven by intersectionn of inequations with axis onlyBgiven by intersection of inequations with X-axis onlyCgiven by corner points of the feasible regionDnone of the above
In the given graph, the feasible region for a LPP is shaded.
The objective function Z = 2x – 3y, will be minimum at:
 View Solution
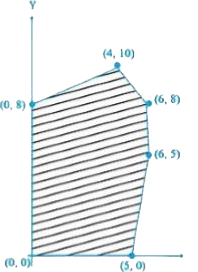
View SolutionIn the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
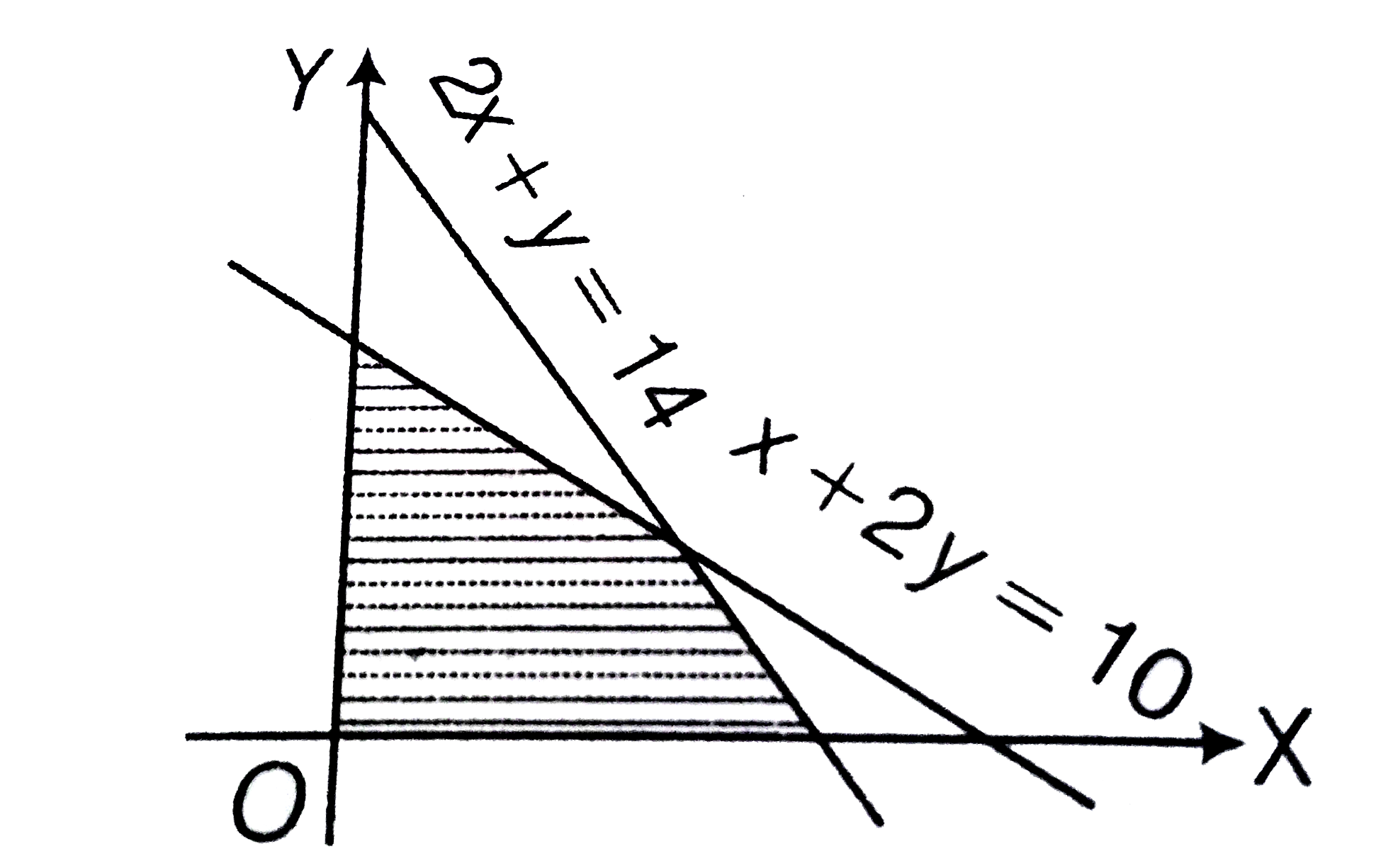
View SolutionThe maximum value of objective function z=2x+3y in the given feasible region is
 View Solution
View SolutionVariables of the objective function of the linear programming problem are
View SolutionIn case of a linear programming problem, feasible region is always
View Solution