Let the function be defined as
f(x)={4x0<x≤1<br>(−4x+5)1<x<2 then limx→1f(x) is :Solution in Tamil
4
does not exist
−4
1
The correct Answer is:B
Step by step video, text & image solution for Let the function be defined as f(x)={4x 0ltxle1(-4x+5) 1ltxlt2 then lim_(xrarr1)f(x) is : by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYBook:PREMIERS PUBLISHERSChapter:DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYExercise:SOLUTION TO EXERCISE 9.6
Explore 25 Videos
- DIFFEREMTIAL CALCULUS DIFFERENTIABILITY AND METHODS OF DIFFERENTITAION Book:PREMIERS PUBLISHERSChapter:DIFFEREMTIAL CALCULUS DIFFERENTIABILITY AND METHODS OF DIFFERENTITAION Exercise:PROBLEMS FOR PRACTICE
Explore 73 Videos
- EXAMINATION QUESTION PAPER MARCH 2019Book:PREMIERS PUBLISHERSChapter:EXAMINATION QUESTION PAPER MARCH 2019Exercise:PART -IV
Explore 4 Videos
Similar Questions
Choose the correct or the most suitable answer from the given four alternatives.
limx→0sinxx
View SolutionIfy=13√x+log5x+8,f∈ddydx.
View SolutionWrite any five different forms of an equation of a straight line.
View SolutionLet f(x)={5x−4,0<x≤14x3−3x,1<x<2.
Find limx→1f(x).
View Solutionफलन f(x)={5x−4,0<x≤14x3−3x,1<x<2 है -
View Solutionयदि f(x)={5x−4,0<x≤14x3−3x,1<x<2
सिद्ध कीजिए की limx→1f(x) एक अस्तित्व है।
View SolutionLet f:[2,∞)→R be the function defined by f(x)=x2−4x+5, then the range of f is
View SolutionThe value of a for which the function f(x)={5x−4if0<x≤14x2+3axif1<x<2} is continous at every point of its domain is
View SolutionShow that f(x)={5x−4, when 0<x≤1,4x3−3x , when 1<x<2 is continuous at x=1.
View SolutionIf function f(x)={(5x-4,यदि 0ltxle1),(4x^(2)+3bx,यदि 1ltxlt2):} Each point of its domain is continuous, so the value of b will be
View Solutionlimx→0f(x)and limx→1f(x)
if f(x)=⎧⎪⎨⎪⎩0⋅x≤0x≤11−2x0<x≤13−4xx>1
View SolutionGiven the function f(x)={−x2ifx≤o, 5x−4if0<x≤1, 4x2−3xif1<x<2, 3x+4ifx≥2 Complete the following table
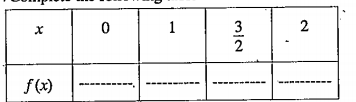
View SolutionIf f(x)={5x−4,0<x≤14x2+3ax,1<x<2
View SolutionLet f:[2,∞)→R be the function defined by f(x)=x2−4x+5. Then the range of f is
View SolutionLet f(x)={5x−4,0<x≤14x3−3x,1<x<2.
Find limx→1f(x).
View Solution