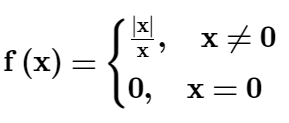Assertion :limx→0sin(1x)=0
Reason: If f,g,h :I≤Rsuch that g(x)≤f(x)≤h(x)for all x in a deleted neighbouhood of xo contained in I and if limx→0g(x)=limx→xoh(x)=l.Then limx→xof(x)=l.[sandwich theorem]
A
R is the best tool to prove A
B
R is not enough to prove A
C
A is not true
D
both A and R are incorrect
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYBOOK - PREMIERS PUBLISHERSCHAPTER - DIFFERENTIAL CALCULUS LIMITS AND CONTINUITYEXERCISE - SOLUTION TO EXERCISE 9.6
25 Videos
- DIFFEREMTIAL CALCULUS DIFFERENTIABILITY AND METHODS OF DIFFERENTITAION BOOK - PREMIERS PUBLISHERSCHAPTER - DIFFEREMTIAL CALCULUS DIFFERENTIABILITY AND METHODS OF DIFFERENTITAION EXERCISE - PROBLEMS FOR PRACTICE
73 Videos
- EXAMINATION QUESTION PAPER MARCH 2019BOOK - PREMIERS PUBLISHERSCHAPTER - EXAMINATION QUESTION PAPER MARCH 2019EXERCISE - PART -IV
4 Videos
Similar Questions
Knowledge Check
limx→0sin|x|x
Ais equal to1Bis equal to 0Cis equal to infinityDdoes not existlimx→0ax−1x is equal to
AaBlog aC0D∞If f(x)={xsin(1x)x≠00x=0 Then, limx→0f(x)
Ais equal to 1Bis equal to−1Cis equal to 0Ddoes not exist