Let the vectors $\to a, \to b, \to c$ be given as $a_{1} ˆ i + a_{2} ˆ j + a_{3} ˆ k, b_{1} ˆ i + b_{2} ˆ j + b_{3} ˆ k$ , $c_{1} ˆ i + (c_{2} ˆ j) + (c_{3} ˆ k)$ .Then show tha $\to a \times (\to b + \to c) = (\to a \times \to b) + (\to a \times \to c$ ).Solution in Tamil

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $= \to a \times \to b + \to a \times \to c$

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Let the vectors veca, vecb, vec c be given as a_(1)hat i + a_(2)hatj + a_(3)hat k, b_(1)hat i + b_(2) hat j + b_(3) hat k, c_(1)hat i + (c_(2)hat j )+( c_(3)hat k).Then show thavec a xx(vec b + vec c) = (vec a xx vec b)+( vec a xx vec c). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.1
2 Videos
VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.2
13 Videos
VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.3
18 Videos
TRIGONOMETRIC FUNCTIONSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - QUESTIONS FROM COMPETITIVE EXAMS
134 Videos

Similar Questions

In the figure which vectors are
(i) equal (ii) collinear (iii) coinitial

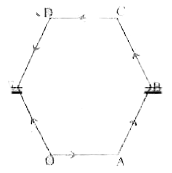
View Solution
Compute the magnitude of the following vectors and identify the unit vector.
$\to a = 2 ˆ i - 3 ˆ j + 5 ˆ k$
View Solution
Find the angle between two vectors $\to a$ and $\to b$ with magnitudes $\sqrt{3}$ and 2, respectivey having $\to a . \to b = \sqrt{6}$ .
View Solution
If $A + B + C = 90^{\circ}$ then
$\frac{cot A + cot B + cot C}{cot A cot B cot C}$ =
View Solution
Let the vectors $\to a, \to b, \to c$ be given as $a_{1} ˆ i + a_{2} ˆ j + a_{3} ˆ k, b_{1} ˆ i + b_{2} ˆ j + b_{3} ˆ k, c_{1} ˆ i + c_{2} ˆ j + c_{3} ˆ k$ . Then show that $\to a \times (\to b + \to c) = \to a \times \to b + \to a \times \to c$
View Solution
Let vec a = hat i + hat j + hat k, vec b = hat i + 4 hat j - hat k, vec c = hat i + hat j + 2 hat k and hat s be a the unit vector the magnitude of the vector (vec a .vec s)(vec b xx vec c) + (vec b. vec s)(vec c xx vec a) + ( vec c.vec s)(vec a xx vec b) is equal to (A) 1 (B) 2 (C) 3 (D) 4
View Solution
Let $\to a = ˆ j - ˆ k$ and $\to c = ˆ i - ˆ j - ˆ k$ . Then vector $\to b$ satisfying $\to a \times \to b + \to c = \to 0$ and $\to a . \to b = 3$ is (1) $2 \to i - \to j + 2 \to k$ (2) $ˆ i - ˆ j - 2 ˆ k$ (3) $ˆ i + j - 2 ˆ k$ (4) $- ˆ i + ˆ j - 2 ˆ k$
View Solution
Let vec b=3hat j+4hat k,vec a=hat i+hat j and let vec b_(1) and vec b_(2) be component of vector b parallel and perpendicular to vec a .If vec b_(1)=(3)/(2)hat i+(3)/(2)hat j then vec b_(2) is equal to
View Solution
Let $\to a = ˆ i + ˆ j + ˆ k, \to b = ˆ i$ and $ˆ c = c_{1} ˆ i + c_{2} ˆ j + c_{3} ˆ k$ . Then, (1)If $c_{1} = 1$ and $c_{2} = 2,$ find $c_{3}$ which makes $\to a, \to b$ and $\to c$ coplanar. (2)If $c_{2} = - 1$ and $c_{3} = 1,$ show that no value of $c_{1}$ can make $\to a, \to b$ and $\to c$ coplanar.
View Solution
If $\to a = a_{1} ˆ i + a_{2} ˆ j + a_{3} ˆ k; \to b = b_{1} ˆ i + b_{2} ˆ j + b_{3} ˆ k, . \to c = c_{1} ˆ i + c_{2} ˆ j + c_{3} ˆ k$ and $[3 \to a + \to b$ $3 \to b + \to c$ $3 \to c + \to a] = 28 [\to a \to b \to c]$ , then find the value of $\frac{λ}{4}$ .
View Solution
If vec(a) = 3 hat(i) + 2 hat(k) , vec(b) = 3hat(j) - hat(k) and vec(c ) = hat(i) + hat(j) + hat(k) . Find ( vec(a) xx vec(b)). vec(c ) .
View Solution
Two balls , having linear momenta vec(p)_(1) = p hat(i) and vec(p)_(2) = - p hat(i) , undergo a collision in free space. There is no external force acting on the balls. Let vec(p)_(1) and vec(p)_(2) , be their final momenta. The following option(s) is (are) NOT ALLOWED for any non -zero value of p , a_(1) , a_(2) , b_(1) , b_(2) , c_(1) and c_(2) (i) vec(p)_(1) = a_(1) hat(i) + b_(1) hat(j) + c_(1) hat(k) , vec(p)_(2) = a_(2) hat(i) + b_(2) hat(j) (ii) vec(p)_(1) = c_(1) vec(k) , vec(p)_(2) = c_(2) hat(k) (iii) vec(p)_(1) = a_(1) hat(i) + b_(1) hat(j) + c_(1) hat(k) ,vec(p)_(2) = a_(2) hat(i) + b_(2) hat(j) - c_(1) hat(k) (iv) vec(p)_(1) = a_(1) hat(i) + b_(1) hat(j) , vec(p)_(2) = a_(2) hat(i) + b_(1) hat(j)
View Solution
If $\to a = a_{1} ˆ i + a_{2} ˆ j + a_{3} ˆ k, \to b = b_{1} ˆ i + b_{2} ˆ j + b_{3} ˆ k$ and $\to c = c_{1} ˆ i + c_{2} ˆ j + c_{3} ˆ k$ prove that $\to a \times (\to b + \to c) = \to a \times \to b + \to a \times \to c$
View Solution
If $ˆ i, ˆ j and ˆ k$ are unit vectors along three mutuaaly perpendicular axes and $\to a = a_{1} ˆ i + a_{2} ˆ j + a_{3} ˆ k, \to b = b_{1} ˆ i + b_{2} ˆ j + b_{3} ˆ k and \to c = c_{1} ˆ i + c_{2} ˆ j + c_{3} ˆ k$ prove that
$\to a . (\to b + \to c) = \to a . \to b + \to a . \to c$
View Solution
If $ˆ i, ˆ j and ˆ k$ are unit vectors along three mutuaaly perpendicular axes and $\to a = a_{1} ˆ i + a_{2} ˆ j + a_{3} ˆ k, \to b = b_{1} ˆ i + b_{2} ˆ j + b_{3} ˆ k and \to c = c_{1} ˆ i + c_{2} ˆ j + c_{3} ˆ k$ prove that
$(\to b + \to c) \times \to a = \to b \times \to a + \to c \times \to a$
View Solution

NEW JOYTHI PUBLICATION-VECTOR ALGEBRA-SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.4

Find |vec a xx vec b| if vec a = hat i -7 hat j + 7 hat k and vec b = ...
02:08
Find a unit vector perpendicular to each of the vector vec a+ vec b a...
04:49
If a unit vector vec a makes angles(pi)/(3) with hat i , (pi)/(4) with...
14:53
Show that (vec a - vec b) xx (vec a + vec b) = 2 (vec a xx vec b)
01:20
Find lambda amd mu if (2 hat i + 6 hat j+ 27 hat k) xx (hat i + lambda...
01:48
Given that vec a. vec b = 0 and vec a xx vec b = vec 0. What can you c...
01:36
Let the vectors veca, vecb, vec c be given as a(1)hat i + a(2)hatj + a...
15:02
If either vec a = vec 0 or vec a xx vec b = vec 0 .Is the converse tr...
05:02
Find the area of the triangle with vertices A(1,1,2)B(2,3,5) and C(1,5...
01:52
Find the area of the parallelogram whose adjacent sides are determined...
02:38
Let the vectorsvec a and vec b be such that |veca| = 3 and |vecb| = (s...
01:58
Area of a rectangle having vertices A,B,C and D with positions vectors...
08:02

Home
Ask Doubt
Profile

Let the vectors →a,→b,→c be given as a1ˆi+a2ˆj+a3ˆk,b1ˆi+b2ˆj+b3ˆk, c1ˆi+(c2ˆj)+(c3ˆk).Then show tha→a×(→b+→c)=(→a×→b)+(→a×→c).Solution in Tamil

The correct Answer is:=→a×→b+→a×→c

Topper's Solved these Questions

Similar Questions

NEW JOYTHI PUBLICATION-VECTOR ALGEBRA-SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.4

Let the vectors $\to a, \to b, \to c$ be given as $a_{1} ˆ i + a_{2} ˆ j + a_{3} ˆ k, b_{1} ˆ i + b_{2} ˆ j + b_{3} ˆ k$ , $c_{1} ˆ i + (c_{2} ˆ j) + (c_{3} ˆ k)$ .Then show tha $\to a \times (\to b + \to c) = (\to a \times \to b) + (\to a \times \to c$ ).Solution in Tamil

The correct Answer is: $= \to a \times \to b + \to a \times \to c$