Let →a,→b,→c be three vectors in the xyz space such that →a×→b=→b×→c=→c×→a≠0 If A, B, C are points with position vector →a,→b,→c respectively, then the number of possible position of the centroid of triangle ABC is -
1
2
3
6
The correct Answer is:A
→a×→b+→c×→b=0 similarly →b+→c=λ2→a
→a+→c=λ1→b →b+→a=λ3→c
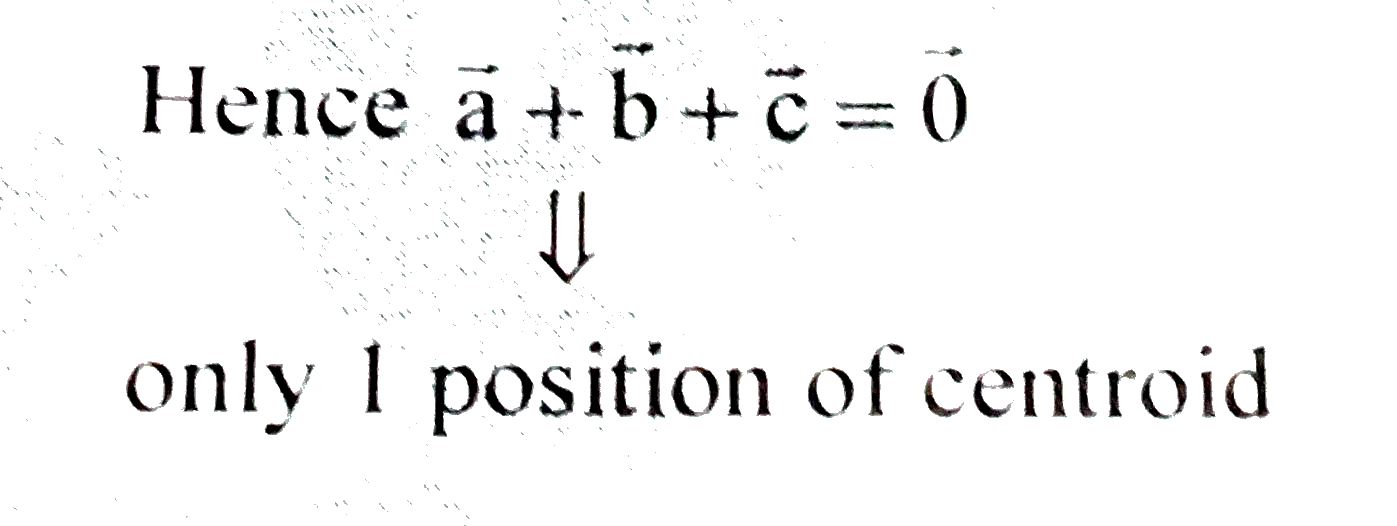
Similar Questions
Let →a,→b,→c be three vectors in the xyz space such that →a×→b=→b×→c=→c×→a≠0 If A,B,C are points with position vectors →a,→b,→c respectively,then the number of possible positions of the centroid of triangle ABC is (A) 1 (B) 2 (C) 3 (D) 6
View SolutionIf →a,→b,→c be three vectors such that [→a→b→c]=4 then [→a×→b→b×→c→c×→a]=
View SolutionLet →a,→b,→c be three vectors from →a×(→b×→c)=(→a×→b)×→c, if
View SolutionIf →a,→b,→c are three vectors such that →a+→b+→c=→0 , then prove that →a×→b=→b×→c=→c×→a
View SolutionIf →a→b→cand→d are vectors such that →a×→b=→c×→dand→a×→c=→b×→d. Then show that the vectors →a−→d and →b−→c are parallel.
View SolutionIf →a×→b=→b×→c=→c×→a then →a+→b+→c=
View SolutionIf →a×→b=→b×→c=→c×→a then →a+→b+→c =
View SolutionIf →a×→b=→b×→c=→c×→a then →a+→b+→c=
View SolutionIf →a,→b,→c are vectors such that [→a→b→c]=4 then find the value of [(→a×→b)(→b×→c)(→c×→a)]
View SolutionIf →a,→b,and→c are three vectors such that →a×→b=→c,→b×→c=→a,→c×→a=→b, then prove that |→a|=∣∣→b∣∣=|→c|.
View Solution
