Let vector →V=(2,3) and vector →U=(6,−4).
(i) What is the resultant of →Uand→V?
To find the resultant of the vectors →U and →V, we will follow these steps:
1. Identify the vectors:
- Given →V=(2,3) can be expressed in vector form as:
→V=2^i+3^j
- Given →U=(6,−4) can be expressed in vector form as:
→U=6^i−4^j
2. Add the vectors:
- The resultant vector →R is given by:
→R=→U+→V
- So we substitute the vector forms:
→R=(6^i−4^j)+(2^i+3^j)
3. Combine the components:
- Combine the ^i components:
6^i+2^i=8^i
- Combine the ^j components:
−4^j+3^j=−1^j
4. Write the resultant vector:
- Therefore, the resultant vector is:
→R=8^i−1^j
Thus, the resultant of →U and →V is →R=8^i−1^j.
- Given →V=(2,3) can be expressed in vector form as:
→V=2^i+3^j
- Given →U=(6,−4) can be expressed in vector form as:
→U=6^i−4^j
- The resultant vector →R is given by:
→R=→U+→V
- So we substitute the vector forms:
→R=(6^i−4^j)+(2^i+3^j)
- Combine the ^i components:
6^i+2^i=8^i
- Combine the ^j components:
−4^j+3^j=−1^j
- Therefore, the resultant vector is:
→R=8^i−1^j
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If vector →v=(1,√3) and vector →u=(3,−2) find the value of |3→v−→u|
A5.4B6C7D7.2 - Question 2 - Select One
The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
A3B4C5D8
Let vector →V=(2,3) and vector →U=(6,−4).
Are →Uand→V perpendicular?View SolutionIf →U=(−1,4) and the resultant of →Uand→V is (4, 5), find →V.
View SolutionA vector →A When added to the vector →B=3ˆi+4ˆj yields a resultant vector that is in the positive y-direction and has a magnitude equal to that of →B. Find the magnitude of →A.
View SolutionThe resultant of two vectors →P and →Q is →R. If →Q is doubled then the new resultant vector is perpendicular to →P. Then magnitude of →R is :-
View SolutionIf a vector →A is parallel to another vector →B then the resultant of the vector →A×→B will be equal to
View SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
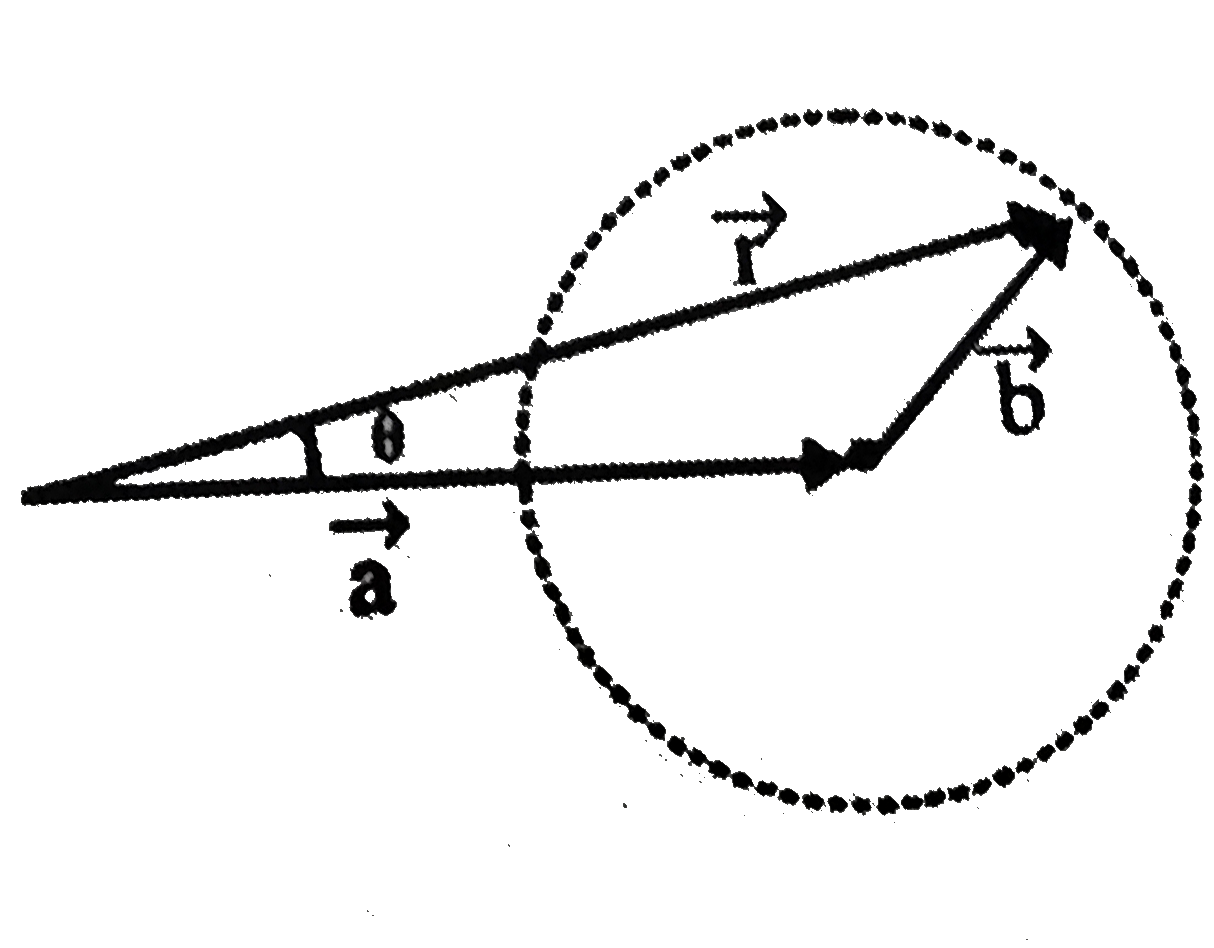 View Solution
View Solution

