If a vector →A is parallel to another vector →B then the resultant of the vector →A×→B will be equal to
A
→A
zero vector
zero
The correct Answer is:C
To solve the problem, we need to analyze the relationship between two vectors, →A and →B, that are parallel to each other. The question asks for the resultant of the cross product →A×→B.
1. Understanding Parallel Vectors:
- When two vectors are parallel, it means they point in the same direction or in exactly opposite directions. Mathematically, if →A is parallel to →B, the angle θ between them is either 0∘ or 180∘.
2. Cross Product Formula:
- The cross product of two vectors →A and →B is given by the formula:
→A×→B=|→A||→B|sin(θ)^n
where |→A| and |→B| are the magnitudes of the vectors, θ is the angle between them, and ^n is the unit vector perpendicular to the plane formed by →A and →B.
3. Substituting the Angle:
- Since →A and →B are parallel, we can substitute θ=0∘ (or 180∘). In both cases, sin(0∘)=0 and sin(180∘)=0.
4. Calculating the Cross Product:
- Plugging in the value of θ:
→A×→B=|→A||→B|sin(0∘)^n=|→A||→B|⋅0⋅^n=0
- Therefore, the cross product →A×→B results in the zero vector.
5. Conclusion:
- The resultant of the vector →A×→B is equal to the zero vector, denoted as →0.
Final Answer:
→A×→B=→0(zero vector)
- When two vectors are parallel, it means they point in the same direction or in exactly opposite directions. Mathematically, if →A is parallel to →B, the angle θ between them is either 0∘ or 180∘.
- The cross product of two vectors →A and →B is given by the formula:
→A×→B=|→A||→B|sin(θ)^n
where |→A| and |→B| are the magnitudes of the vectors, θ is the angle between them, and ^n is the unit vector perpendicular to the plane formed by →A and →B.
- Since →A and →B are parallel, we can substitute θ=0∘ (or 180∘). In both cases, sin(0∘)=0 and sin(180∘)=0.
- Plugging in the value of θ:
→A×→B=|→A||→B|sin(0∘)^n=|→A||→B|⋅0⋅^n=0
- Therefore, the cross product →A×→B results in the zero vector.
- The resultant of the vector →A×→B is equal to the zero vector, denoted as →0.
→A×→B=→0(zero vector)
Similar Questions
Two vectors →Aand→B lie in plane, another vector →C lies outside this plane, then the resultant of these three vectors i.e., →A+→B+→C
View SolutionTwo vectors →A and →B lie in X-Y plane. The vector →B is perpendicular to vector →A. If →A=ˆi+ˆj, then →B may be :
View SolutionA vector →A of length 10 units makes an angle of 60∘ with a vector →B of length 6 units. Find the magnitude of the vector difference →A−→B & the angles with vector →A.
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
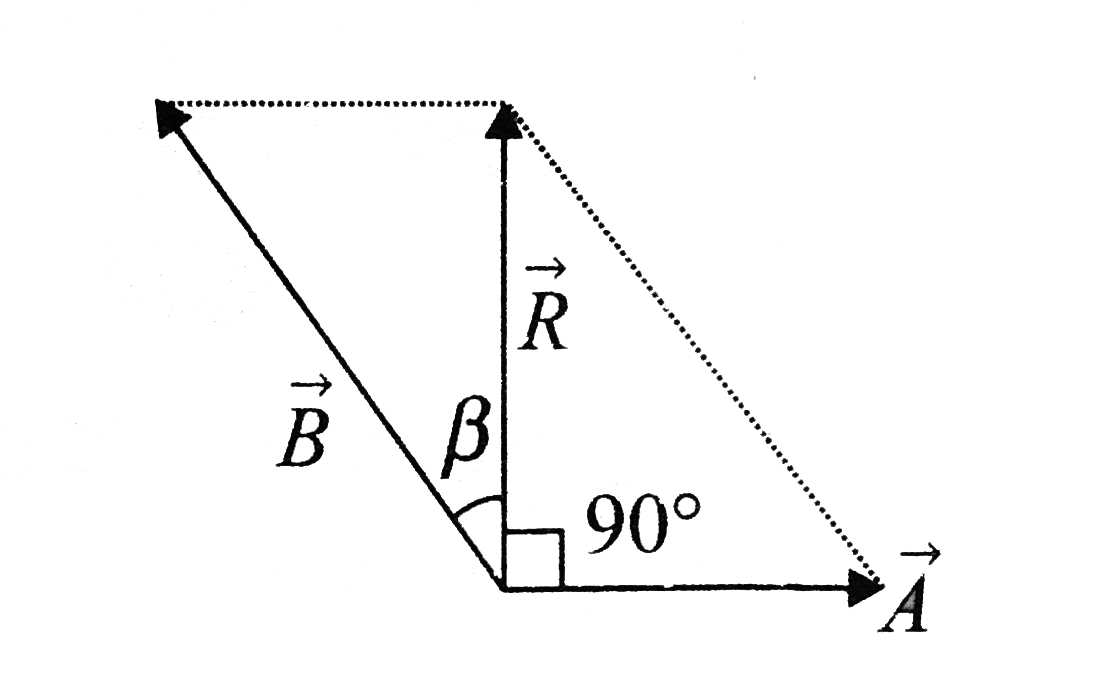
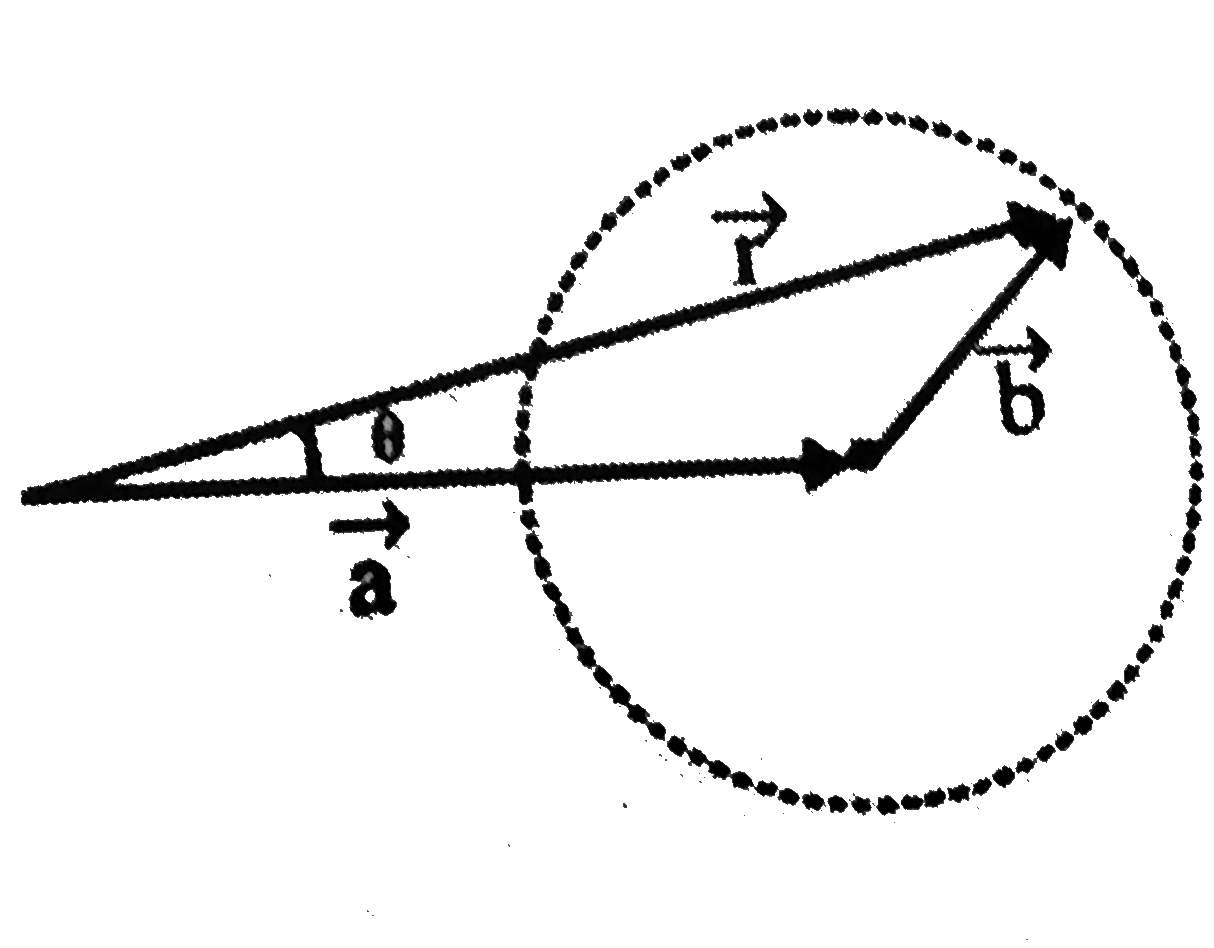
View SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
View SolutionA vector →A When added to the vector →B=3ˆi+4ˆj yields a resultant vector that is in the positive y-direction and has a magnitude equal to that of →B. Find the magnitude of →A.
View SolutionUnit vector parallel to the resultant of vectors →A=4ˆi−3ˆj and →B=8ˆi+8ˆj will be
View SolutionIf the vectors →a+→b,→b+→c and →c+→a are coplanar, then prove that the vectors →a,→b and →c are also coplanar.
View SolutionIf →A and →B are two vectors, then the correct relation is :
View SolutionThe angle between vectors →Aand→B is 60∘ What is the ratio →A.→B and ∣∣→A×→B∣∣
View Solution
