Let X be a discrete random variable whoose probability distribution is defined as follows.
P(X=x)=⎧⎪⎨⎪⎩k(x+1),for x=1,2,3,42kx, for x=5,6,70, otherwise
where,k is a constant. Calculate (i) the value of k. (ii) E (X).
(ii) standard deviation of X.
P(X=x)=⎧⎪⎨⎪⎩k(x+1),for x=1,2,3,42kx, for x=5,6,70, otherwise
Thus, we have following table

(i) since, ∑Pi=1
⇒k(2+3+4+5+10+12+14)=1⇒k=150
(ii) ∵E(X)=∑XP(X)
∴E(X)=2k+6k+12k+20k+50k+72k+98k+0=260k
=260×150=265=5.2 [∵k=150] ....(i)
(iii) We know that,
Var(X)=[E(X2)]−[E(X)]2=∑X2P(X)−[∑{XP(X)}]2
=[2k+12k+36k+80K+250k+432k+686k+0]−[5.2]2 [using Eq. (i)]
=[1498k]−27.04=[1498×150]−27.04 [∵k=150]
=29.96-27.04=2.92
We know that , standard deviation of X=√Var(X)=√2.92−1.7088=1.7(approx)
Topper's Solved these Questions
Similar Questions
Let X be a discrete random variable whose probability distribution is defined as follows: P(X=x)={k(x+1)forx=1,2,3,42kxforx=5,6,70otherwise , where k is a constant. Find (i) k (ii) E(X) (iii) standard deviation of X.
View SolutionThe probability distribution of a random variable x is given as under
P(X=x)=⎧⎪⎨⎪⎩kx2x=1,2,32kxx=4,5,60,otherwise
where, k is a constant. Calculate
(i) E(X) (ii) E(3X2) (iii) P(X≥4)
View Solution
Knowledge Check
If X is the a random variable with probability mass function P(x)=kx, for x = 1,2,3
= 0 , otherwise
then k = ……..A15B14C16D23
The probability distribution of a random variable x is given as under
P(X=x)=⎧⎪⎨⎪⎩kx2x=1,2,32kxx=4,5,60,otherwise
where, k is a constant. Calculate
(i) E(X) (ii) E(3X2) (iii) P(X≥4)
View SolutionA random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionIf X is a random variable with probability distribution P(X=k)=(k+1)C2k,K=0,1,2,…. then find C.
View SolutionA random variable X has the following probability distribution:
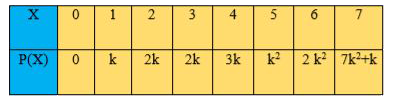
Determine : (i) k (ii) P(X<3) (iii) P(X>4)
View SolutionThe probability distribution of a random variable X is given as under: P(X=x)={kx2forx=1,2,32kxforx=4,5,60otherwise , where k is a constant. Find (i) P(X≥4 ) (ii) E(X) (iii) E(3X2)
View SolutionThe probability distribution of a random variable X is given as under: P(X=x)={kx2forx=1,2,32kxforx=4,5,60otherwise , where k is a constant. Find (i) P(X≥4 ) (ii) E(X) (iii) E(3X2)
View SolutionThe random variable X has a probability distribution P(X) of the following form, where k is some arbitary real number:
P(X=x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩k,if x=02k,if x=13k,if x=20,otherwise
(i) Determine the value of k (ii) Find P(X<2),P(X≤2),P(X≥2)
View Solution
